
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.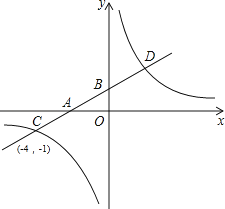
(1)求反比例函数与一次函数的解析式;
(2)若点P为坐标轴上一点,且S△ACP=2S△ABO , 请直接写出点P的坐标.
【答案】
(1)
解:∵点C坐标为(﹣4,﹣1)在反比例函数y= ![]() 的图象上,
的图象上,
∴﹣1= ![]() ,
,
解得:n=4,
∴反比例函数的解析式为:y= ![]() ;
;
∵点D的横坐标为2,
∴y= ![]() =2,
=2,
∴点D(2,2),
将点C与D代入一次函数解析式,可得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式的解析式为:y= ![]() x+1;
x+1;
(2)
解:如图

∵一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,
∴A(﹣2,0),B(0,1),
∴S△ABO= ![]() ×2×1=1,
×2×1=1,
∴S△ACP=2S△ABO=2,
若点P在x轴上,则AP=4,
∴点P的坐标为:(﹣6,0)或(2,0),
若点P在y轴上,则S△ACP=S△BCP﹣S△ABP= ![]() ×4×BP﹣
×4×BP﹣ ![]() ×BP×2=2,
×BP×2=2,
∴BP=2,
∴点P(0,3)或(0,﹣1).
综上可得:点P的坐标为:(﹣6,0),(2,0),(0,3)或(0,﹣1).
【解析】(1)由一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.


科目:初中数学 来源: 题型:
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( ![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)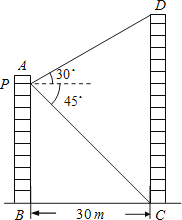
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
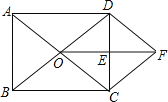
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).

(1)在如图所示的平面直角坐标系画出该四边形;
(2)四边形ABCD的面积是________;
(3)四边形ABCD内(边界点除外)一共有_____个整点(即横坐标和纵坐标都是整数的点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形且AB=AC,BD是⊙O的直径,过点A做AP∥BC交DB的延长线于点P,连接AD.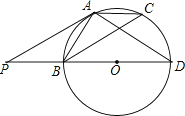
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是2,cos∠ABC= ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
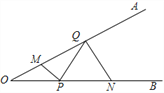
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com