
����Ŀ���ھ���ABCD�У���AD=8��������ABCD�۵���ʹ�õ�B����CD���ϵĵ�P������ͼ1����
��1����ͼ2�����ۺ����BC���ڵ�O�����ӣ�OP��OA����֪��OCP���PDA�������Ϊ1��4�����AB�ij���
��2������M���߶�AP�ϣ������P��A�غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��CA�����ڵ�F������M��ME��BP�ڵ�E��
����ͼ1�л���ͼ�Σ�
���ڡ�OCP���PDA�������Ϊ1��4���������£����ʶ���M��N���ƶ��Ĺ����У��߶�EF�ij����Ƿ����仯������˵�����ɣ�
���𰸡��⣺��1����ͼ2�����ı���ABCD�Ǿ��Σ�
���C=��D=90�㣬
���1+��3=90�㣬
�����۵��ɵá�APO=��B=90�㣬
���1+��2=90�㣬
���2=��3��
�֡ߡ�D=��C��
���OCP�ס�PDA��
�ߡ�OCP���PDA�������Ϊ1��4��
��![]() =
=![]()
��CP=![]() AD=4��
AD=4��
��OP=x����CO=8��x��
��Rt��PCO�У���C=90�㣬
�ɹ��ɶ����� x2=��8��x��2+42 ��
��ã�x=5��
��AB=AP=2OP=10��
���AB�ij�Ϊ10��
��2������ͼ���£�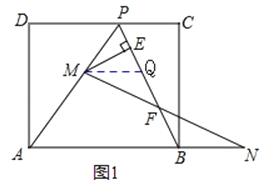
����MQ��AN����PB�ڵ�Q����ͼ1��
��AP=AB��MQ��AN��
���APB=��ABP����ABP=��MQP��
���APB=��MQP��
��MP=MQ��
��MP=MQ��ME��PQ��
��PE=EQ=![]() PQ��
PQ��
��BN=PM��MP=MQ��
��BN=QM��
��MQ��AN��
���QMF=��BNF��
�ڡ�MFQ�͡�NFB�У�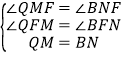 ��
��
���MFQ�ա�NFB��
��QF=BF��
��QF=![]() QB��
QB��
��EF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB��
PB��
�ɣ�1���еĽ��ۿɵã�
PC=4��BC=8����C=90�㣮
��PB=![]() =4
=4![]() ��
��
��EF=![]() PB=2
PB=2![]() ��
��
�൱��M��N���ƶ������У��߶�EF�ij��Ȳ��䣬����Ϊ2![]() ��
��
����������1���������������Ρ�OCP�ס�PDA���������PC���Լ�AP��OP�Ĺ�ϵ��Ȼ����Rt��PCO�����ù��ɶ������OP�����Ӷ����AB����
��2���ٸ�����������ͼ�Σ�
���ɱ���ȳ������뵽ȫ�ȣ���BN��PM���ڵ������β���ȫ�ȣ����������߶ε�λ�úܲ�Э������ͨ����ƽ���߹���ȫ�ȣ�Ȼ������������ȫ�ȼ����������ε����ʼ����Ƴ�EF��PB��һ�룬ֻ�����PB���Ϳ������EF����
�����㾫����������Ĺؼ�����������κ���ͼ���ƽ�Ƶ����֪ʶ������ƽ�Ʋ��裺��1���䷽ y=a(x-h)2+k��ȷ�����㣨h,k����2����x������Ҽ�����y���ϼ��¼���


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=12��BC=15��AD��BC�ڵ�D����BAD=30�㣬��tanC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=45������M��N�ڱ�OA�ϣ�OM=3��ON=7����P��ֱ��OB�ϵĵ㣬Ҫʹ��P��M��N���ɵ��������εĵ�P�У�����������
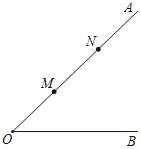
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���OΪֱ��AB��һ�㣬����O������OC��ʹ��AOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
��1����ͼ���е����ǰ�OMN�ڷų���ͼ����ʾ��λ�ã�ʹһ��OM�ڡ�BOC���ڲ�����OMƽ�֡�BOCʱ����BON=�� ������ֱ��д�������
��2���ڣ�1���������£����߶�NO���ӳ���OP����ͼ����ʾ������˵������OP�ǡ�AOC��ƽ���ߣ�
��3����ͼ���е����ǰ�OMN�ڷų���ͼ����ʾ��λ�ã���̽����NOC���AOM֮���������ϵ����ֱ��д�����������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P��y�������ڵ�C����P�İ뾶��4��ֱ��y=x����P�صõ���AB�ij�Ϊ4![]() �� ���P�����꣮
�� ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ������ֱ�������ΰ�ͼʾ��ʽ���η��ۣ���DE��a�����DC��ƽ�֡�BDE����BC��Ϊ![]() ��1��a���ۡ�BC��D�ǵ��������Σ��ܡ�CED���ܳ�����BC�ij�����������������ȷ�������_______��
��1��a���ۡ�BC��D�ǵ��������Σ��ܡ�CED���ܳ�����BC�ij�����������������ȷ�������_______��
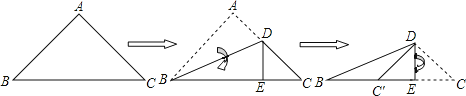
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�AD��BC������D��DF��BC��F����AD=2��BC=4��DF=2����DC�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����һ�����η羰������ABCD����AB=50�ף���BC=25�ף�Ϊ�������˹��ͣ�������������ͼ��ʾ��С·��ͼ�з���Ӱ���֣���С·�Ŀ���Ϊ1�ף���С������С·���м䣬�ӳ���A������B���ߵ�·�ߣ�ͼ�����ߣ���Ϊ�� ��

A��100�� B��99�� C��98�� D��74��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ABCD��һ����OΪֱ�Ƕ��������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD������M��N��
��1����ͼ1������O���A�غϣ���OM��ON��������ϵ��__________________��
��2����ͼ2������O�������ε����ģ������Խ��ߵĽ���������1���еĽ����Ƿ���Ȼ��������˵��������
��3����ͼ3������O�������ε��ڲ������߽�������OM=ONʱ����̽����O���ƶ������п��γ�ʲôͼ�Σ�
��4����ͼ4�ǵ�O���������ⲿ��һ���������OM=ONʱ������͡���O��λ���ڸ�������£����ⲿ���ƶ����γɵ�ͼ�Ρ����һ����ȷ�Ľ��ۣ�������˵����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com