
【题目】如图,△ABC中,CD是边AB上的高,且![]() .
.
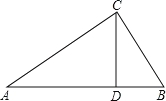
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明家承包的果园,前年水果产量为50吨,后来改进了种植技术,今年的总产量是60.5吨,小明家去年,今年平均每年的粮食产量增长率是( )
A.5%
B.10%
C.15%
D.20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由. 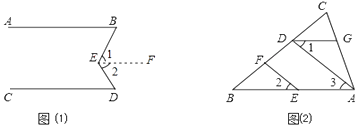
(1)完成正确的证明:如图(1),已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1=()
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2=()
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
(2)如图(2),在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.()
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥()
所以∠BAC+=180° ().
又因为∠BAC=70°,所以∠AGD=110°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=4cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒后⊙P与直线CD相切.
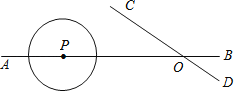
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.据此规律计算:每件商品降价元时,商场日盈利可达到2100元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com