
分析 (1)根据题目中的信息可以解答本题;
(2)根据题目给出的信息可以解答本题,然后选择一空说明理由即可.
解答 解:(1)①∵34=81,∴log381=4;
②∵31=3,∴log33=1;
③∵30=1,∴log31=0;
④∵24=16,∴logX16=4时,x=2;
故答案为:①4;②1;③0;④2;
(2)由题目中的信息可得,logaM1M2M3…Mn=logaM1+logaM2+logaM3+…+logaMn,
loga$\frac{M}{N}$=logaM-logaN,
故答案为:logaM1+logaM2+logaM3+…+logaMn,logaM-logaN;
loga$\frac{M}{N}$=logaM-logaN,
理由:设ax=M,ay=N,则logaM=x,logaN=y(a>0,a≠1,M、N均为正数),
∵ax÷ay=ax-y,∴ax-y=M÷N∴loga$\frac{M}{N}$=x-y,
即loga$\frac{M}{N}$=logaM-logaN.
点评 本题考查整式的混合运算,解题的关键是明确题意,可以利用新定义进行解答问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
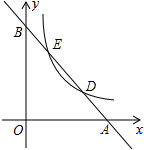 如图,已知直线l:y1=kx+b分别与x轴、y轴交于A、B两点,与双曲线y2=$\frac{a}{x}$(a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)
如图,已知直线l:y1=kx+b分别与x轴、y轴交于A、B两点,与双曲线y2=$\frac{a}{x}$(a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com