
| ���� | ���� | |
| �۸���Ԫ/̨�� | 12 | 10 |
| ��������/�£� | 240 | 180 |
���� ��1�����ʡ��Դ�����豸�����豸x̨�������豸��10-x��̨�����ݸù�˾��������豸���ʽ���110��Ԫ���г�����ʽ�����x��ֵ���ɵó��𰸣�
��2�����ݼ��͡����͵IJ�����˾Ҫ��ÿ�µIJ���������2040�֣��г�����ʽ�����x��ֵ��ȷ����������Ȼ����бȽϼ��ɣ�
��� �⣺��1���蹺���ʡ��Դ�����豸�����豸x̨�������豸��10-x��̨����������ã�
12x+10��10-x����110��
��ã�x��5��
��xȡ�Ǹ�������
��x=0��1��2��3��4��5��
����6�ֹ�����
��2�������⣺240x+180��10-x����2040��
��ã�x��4��
��xΪ4��5��
��x=4ʱ�������ʽ�Ϊ��12��4+10��6=108����Ԫ����
��x=5ʱ�������ʽ�Ϊ��12��5+10��5=110����Ԫ����
����ʡǮ�Ĺ���Ϊ��Ӧѡ�������豸4̨�������豸6̨��
���� ���⿼��һԪһ�β���ʽ��Ӧ�ã��������Ĺؼ��Ƕ������⣬�ҵ���������IJ��ȹ�ϵʽ��Ҫ���÷����˼����������÷��������⣮


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ�����ε�̺ABCD���������п��ȶ���1�Ļ��ߣ�����ε�̺AB�߳�Ϊx�ף����л��ߺ�������̺EFGH��FG�߳�Ϊy�ף�
��һ�����ε�̺ABCD���������п��ȶ���1�Ļ��ߣ�����ε�̺AB�߳�Ϊx�ף����л��ߺ�������̺EFGH��FG�߳�Ϊy�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
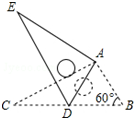 ��ͼ����Rt��ABC�Ƶ�A��˳ʱ����תһ���Ƕȵõ�Rt��ADE����B�Ķ�Ӧ��Dǡ������BC���ϣ���BC=2$\sqrt{3}$����B=60�㣬��CD�ij�Ϊ$\sqrt{3}$��
��ͼ����Rt��ABC�Ƶ�A��˳ʱ����תһ���Ƕȵõ�Rt��ADE����B�Ķ�Ӧ��Dǡ������BC���ϣ���BC=2$\sqrt{3}$����B=60�㣬��CD�ij�Ϊ$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��AD�ǡ�ABC�ĸߣ�BEƽ�֡�ABC��AD��E������C=70�㣬��BED=68�㣬���BAC�Ķ�����
��֪����ͼ��AD�ǡ�ABC�ĸߣ�BEƽ�֡�ABC��AD��E������C=70�㣬��BED=68�㣬���BAC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
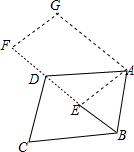 ��ͼ����ƽ���ı���ABCD�Ƶ�A��ת��ƽ���ı���AEFG��λ�ã����е�B��C��D�ֱ����ڵ�E��F��G�����ҵ�B��E��D��F��һֱ���ϣ������Eǡ���ǶԽ���BD���е㣬��ô$\frac{AB}{AD}$��ֵ��$\frac{\sqrt{2}}{2}$��
��ͼ����ƽ���ı���ABCD�Ƶ�A��ת��ƽ���ı���AEFG��λ�ã����е�B��C��D�ֱ����ڵ�E��F��G�����ҵ�B��E��D��F��һֱ���ϣ������Eǡ���ǶԽ���BD���е㣬��ô$\frac{AB}{AD}$��ֵ��$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com