
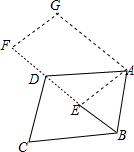
 如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.
如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$. 分析 先利用旋转的性质得∠1=∠2,BE=$\frac{1}{2}$BD,AB=AE,再证明∠1=∠3,则可判断△BAE∽△BDA,利用相似比可得$\frac{AB}{BD}$=$\frac{\sqrt{2}}{2}$,然后证明AD=BD即可得到$\frac{AB}{AD}$的值.
解答 解:∵平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,点E恰好是对角线BD的中点,
∴∠1=∠2,BE=$\frac{1}{2}$BD,AB=AE,
∵EF∥AG,
∴∠2=∠3,
∴∠1=∠3,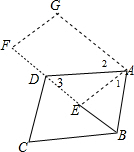
∵∠ABE=∠DBA,
∴△BAE∽△BDA,
∴AB:BD=BE:AB,∠AEB=∠DAB,
∴AB2=$\frac{1}{2}$BD2,
∴$\frac{AB}{BD}$=$\frac{\sqrt{2}}{2}$,
∵AE=AB,
∴∠AEB=∠ABD,
∴∠ABD=∠DAB,
∴DB=DA,
∴$\frac{AB}{AD}$=$\frac{\sqrt{2}}{2}$.
故答案为$\frac{\sqrt{2}}{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△BAE∽△BDA,


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
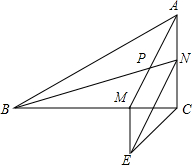 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
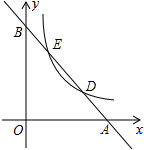 如图,已知直线l:y1=kx+b分别与x轴、y轴交于A、B两点,与双曲线y2=$\frac{a}{x}$(a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)
如图,已知直线l:y1=kx+b分别与x轴、y轴交于A、B两点,与双曲线y2=$\frac{a}{x}$(a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com