
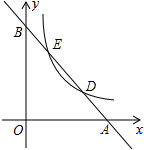
 ��ͼ����ֱ֪��l��y1=kx+b�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y2=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣮����D������Ϊ��4��1������E������Ϊ��1��4��
��ͼ����ֱ֪��l��y1=kx+b�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y2=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣮����D������Ϊ��4��1������E������Ϊ��1��4������ ��1������ֱ��l��y1=kx+b��˫����y2=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣬��D������Ϊ��4��1������E������Ϊ��1��4�������Էֱ����ֱ��l��˫���ߵĽ���ʽ��
��2��������������г���Ӧ�ķ����飬Ȼ�����ֱ��l��˫��������ֻ��һ�����㣬��֪������ķ���������ɵĶ�Ԫһ�η����С�=0��ע�⽻���ڵ�һ���ޣ�
��3�����ݺ���ͼ����Եõ���y1��y2ʱ��x��ȡֵ��Χ��
��� �⣺��1����ֱ��l��y1=kx+b��˫����y2=$\frac{a}{x}$��a��0��x��0���ֱ���D��E���㣬��D������Ϊ��4��1������E������Ϊ��1��4����
��$\left\{\begin{array}{l}{4k+b=1}\\{k+b=4}\end{array}\right.$��$4=\frac{a}{1}$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$��a=4��
��ֱ��l��y1=-x+5��˫����y2=$\frac{4}{x}$��
�ʴ�Ϊ��y1=-x+5��y2=$\frac{4}{x}$��
��2��������ɵã�
$\left\{\begin{array}{l}{{y}_{2}=\frac{4}{x}}\\{{y}_{1}=-x+5-m}\end{array}\right.$
����
x2+��m-5��x+4=0��
��ֱ��l��˫��������ֻ��һ�����㣬
�ࣨm-5��2-4��1��4=0��
��ã�m=1��m=9
��m=1ʱ��ֱ����˫���ߵ�һ�������ڵ�һ���ޣ���m=9ʱ��ֱ����˫����һ�������ڵ������ޣ�˫����y2=$\frac{a}{x}$��a��0��x��0��
��m=1��
����mΪ1ʱ��ֱ��l��˫��������ֻ��һ�����㣻
��3����ͼ���֪����0��x��1��x��4ʱ��y1��y2��
�ʴ�Ϊ��0��x��1��x��4��
���� ���⿼�鷴����������һ�κ����Ľ������⣬����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
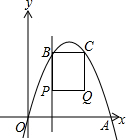 ��ͼ����ƽ��ֱ������ϵ�У�����ԭ���������y=-x2+4mx��m��0����x�����һ������Ϊ��A������P��1��m����ֱ��PB��x�ᣬ���������ڵ�B������B���������߶Գ���ĶԳƵ�C����B��C���غϣ�������BC������P��B���غ�ʱ����BP��BCΪ��������PBCQ�������PBCQ���ܳ�Ϊl��
��ͼ����ƽ��ֱ������ϵ�У�����ԭ���������y=-x2+4mx��m��0����x�����һ������Ϊ��A������P��1��m����ֱ��PB��x�ᣬ���������ڵ�B������B���������߶Գ���ĶԳƵ�C����B��C���غϣ�������BC������P��B���غ�ʱ����BP��BCΪ��������PBCQ�������PBCQ���ܳ�Ϊl���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
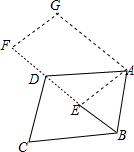 ��ͼ����ƽ���ı���ABCD�Ƶ�A��ת��ƽ���ı���AEFG��λ�ã����е�B��C��D�ֱ����ڵ�E��F��G�����ҵ�B��E��D��F��һֱ���ϣ������Eǡ���ǶԽ���BD���е㣬��ô$\frac{AB}{AD}$��ֵ��$\frac{\sqrt{2}}{2}$��
��ͼ����ƽ���ı���ABCD�Ƶ�A��ת��ƽ���ı���AEFG��λ�ã����е�B��C��D�ֱ����ڵ�E��F��G�����ҵ�B��E��D��F��һֱ���ϣ������Eǡ���ǶԽ���BD���е㣬��ô$\frac{AB}{AD}$��ֵ��$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
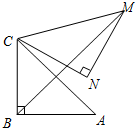 ��ͼ��Rt��ABC�У���ABC=90�㣬AB=BC=2������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������BM����ôBM�ij���$\sqrt{6}+\sqrt{2}$��
��ͼ��Rt��ABC�У���ABC=90�㣬AB=BC=2������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������BM����ôBM�ij���$\sqrt{6}+\sqrt{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com