
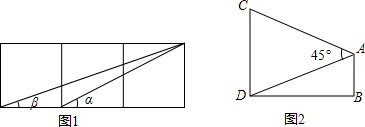
分析 (1)利用tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$,tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$计算即可;
(2)由根与系数的关系得出tanα+tanβ=$\frac{3}{2}$,tanα•tanβ=$\frac{1}{2}$,再代入tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$,计算即可求解;
(3)①利用网格结构,根据正切函数的定义得出tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,然后求出tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1,即可证明α+β=45°;
②过A作AE⊥CD于E,则ABDE是矩形,DE=AB=9,CE=6.设BD=AE=xm,∠CAE=α,∠DAE=β,根据正切函数的定义得出tanα=$\frac{CE}{AE}$=$\frac{6}{x}$,tanβ=$\frac{DE}{AE}$=$\frac{9}{x}$.由tan(α+β)=tan45°=1,得出方程$\frac{\frac{6}{x}+\frac{9}{x}}{1-\frac{6}{x}•\frac{9}{x}}$=1,解方程即可.
解答 (1)解:tan75°=tan(30°+45°)=$\frac{\frac{\sqrt{3}}{3}+1}{1-\frac{\sqrt{3}}{3}×1}$=$\frac{\sqrt{3}+3}{3-\sqrt{3}}$=2+$\sqrt{3}$;
tan15°=tan(45°-30°)=$\frac{1-\frac{\sqrt{3}}{3}}{1+1×\frac{\sqrt{3}}{3}}$=$\frac{3-\sqrt{3}}{3+\sqrt{3}}$=2-$\sqrt{3}$.
故答案为2+$\sqrt{3}$;2-$\sqrt{3}$;
(2)解:∵tanα,tanβ是方程2x2-3x+1=0的根,
∴tanα+tanβ=$\frac{3}{2}$,tanα•tanβ=$\frac{1}{2}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{\frac{3}{2}}{1-\frac{1}{2}}$=3;
(3)①证明:∵tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=$\frac{\frac{5}{6}}{\frac{5}{6}}$=1,
∴α+β=45°;
②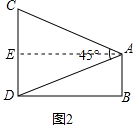 解:如图,过A作AE⊥CD于E,则ABDE是矩形,DE=AB=9,CE=CD-DE=15-9=6.
解:如图,过A作AE⊥CD于E,则ABDE是矩形,DE=AB=9,CE=CD-DE=15-9=6.
设BD=AE=xm,∠CAE=α,∠DAE=β,α+β=∠CAD=45°.
在Rt△CAE中,tanα=$\frac{CE}{AE}$=$\frac{6}{x}$,
在Rt△DAE中,tanβ=$\frac{DE}{AE}$=$\frac{9}{x}$.
∵tan(α+β)=tan45°=1,
∴$\frac{\frac{6}{x}+\frac{9}{x}}{1-\frac{6}{x}•\frac{9}{x}}$=1,
整理得x2-15x-54=0,
解得x1=18,x2=-3(不合题意舍去),
经检验,x=18是原方程的根,也符合题意.
答:建筑物AB和CD的底部之间的距离BD为18m.
点评 本题考查了解直角三角形的应用,根与系数的关系,正切函数的定义,理解公式tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$,tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$,并且能够灵活运用是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:填空题
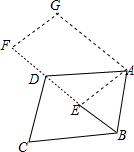 如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.
如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )| A. | -1≤b≤$\frac{1}{2}$ | B. | -1≤b≤1 | C. | -$\frac{1}{2}$≤b≤1 | D. | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
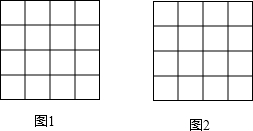 如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com