
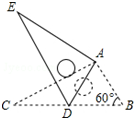
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$. 分析 直接利用旋转的性质得出对应边相等,进而利用等边三角形的判定与性质得出AB=AD=BD,AB=$\frac{1}{2}$BC,进而求出答案.
解答 解:∵将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.
∴AD=AB,
∵∠B=60°,
∴△ADB是等边三角形,∠C=30°,
∴AB=AD=BD,AB=$\frac{1}{2}$BC,
∴AD=BD=$\frac{1}{2}$BC,
∴CD=$\frac{1}{2}$BC=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题主要考查了旋转的性质以及等边三角形的判定与性质,得出△ADB是等边三角形是解题关键.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{m=2}\\{n=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=-2}\\{n=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=1}\\{n=-\frac{7}{3}}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
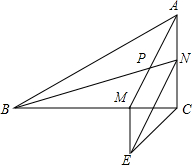 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
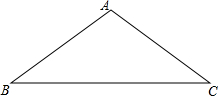 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com