
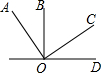
 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.  提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
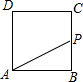 如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )
如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )| A. | 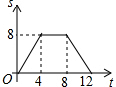 | B. | 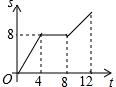 | C. | 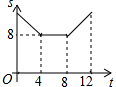 | D. | 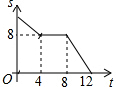 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.
在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
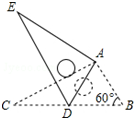 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
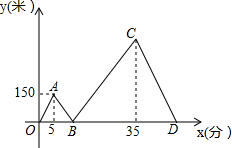 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com