
����Ŀ����ͼ����ֱ֪��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�B��������
��x�ύ�ڵ�C����y�ύ�ڵ�B��������![]() ����B��C���㣮
����B��C���㣮
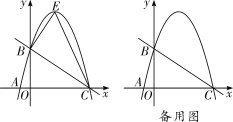
��1���������ߵĽ���ʽ��
��2����ͼ����E��ֱ��BC�Ϸ��������ϵ�һ���㣬��![]() ������ʱ���������E�����ꣻ
������ʱ���������E�����ꣻ
��3���ڣ�2���Ľ����£�����E��y���ƽ���߽�ֱ��BC�ڵ�M������AM����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2����
����2����![]() ʱ��
ʱ��![]() �����ֵ����ʱ
�����ֵ����ʱ![]() ����3��
����3��![]() ��
��![]() ��
��![]() ��
��
��������
(1��Ҫ�������ߵĽ���ʽ���ȸ���һ�κ������B�͵�C�����꣬�����ô���ϵ����������κ����Ľ���ʽ����2��Ҫ��![]() ������ʱ����E�����꣬���ȹ���E��
������ʱ����E�����꣬���ȹ���E��![]() �ᣬ��ֱ��BC�ڵ�G�������E�����꣬��ʾ����G�����꣬Ȼ���ʾ��EG�ij������������������ʽ�����κ�������ֵ���ɵó���E�����ꣻ��3��Ҫ��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��εĵ�P�����꣬���������������AMΪ��ʱ���ı���AMQP��ƽ���ı��Σ�����AMΪ�ߣ��ı���AMPQ��ƽ���ı��Σ�����AMΪ�Խ���ʱ���ı���APMQ��ƽ���ı��Σ�����ƽ���ı��ε����������������P�����꣮
�ᣬ��ֱ��BC�ڵ�G�������E�����꣬��ʾ����G�����꣬Ȼ���ʾ��EG�ij������������������ʽ�����κ�������ֵ���ɵó���E�����ꣻ��3��Ҫ��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��εĵ�P�����꣬���������������AMΪ��ʱ���ı���AMQP��ƽ���ı��Σ�����AMΪ�ߣ��ı���AMPQ��ƽ���ı��Σ�����AMΪ�Խ���ʱ���ı���APMQ��ƽ���ı��Σ�����ƽ���ı��ε����������������P�����꣮
�⣺��1����![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() �����
�����![]() ����
����![]() ��
��
��![]() ��
��![]() ����������
����������![]() �еã�
�еã�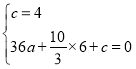 ���
���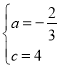 ��
��
�������ߵĽ���ʽΪ![]() ��
��
��2�����ͼ�٣�����E��![]() �ᣬ��ֱ��BC�ڵ�G��
�ᣬ��ֱ��BC�ڵ�G��
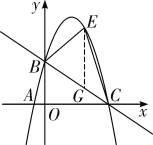 ͼ��
ͼ��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
�൱![]() ʱ��
ʱ��![]() �����ֵ�����ʱ
�����ֵ�����ʱ![]() ��
��
��3�����ڣ���P��������![]() ��
��![]() ��
��![]() ��
��
[�ⷨ��ʾ]
![]() ��
��
�Գ�����ֱ��![]() ����
����![]() ��
��
�ߵ�Q�������߶Գ����ϵĶ��㣬���Q�ĺ�����Ϊ![]() ��
��
���������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�
�����ͼ�ڣ���AMΪ��ʱ���ı���AMQP��ƽ���ı��Σ��ɣ�2���ɵõ�M�ĺ�������3��
�ߵ�M��ֱ��![]() �ϣ����M��������
�ϣ����M��������![]() ���֡ߵ�A��������
���֡ߵ�A��������![]() ����Q�ĺ�����Ϊ
����Q�ĺ�����Ϊ![]() �����ݵ�M����Q��ƽ�ƹ��ɿ�֪��P�ĺ�����Ϊ
�����ݵ�M����Q��ƽ�ƹ��ɿ�֪��P�ĺ�����Ϊ![]() ����
����![]() ��
��
�����ͼ�ۣ���AMΪ��ʱ���ı���AMPQ��ƽ���ı��Σ�
�ɣ�2���ɵõ�M�ĺ�������3��
��![]() ���ҵ�Q�ĺ�����Ϊ
���ҵ�Q�ĺ�����Ϊ![]() ��
��
���ݵ�A����Q��ƽ�ƹ��ɿ�֪��P�ĺ�����Ϊ![]() ����
����![]() ��
��
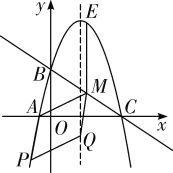 ͼ��
ͼ�� 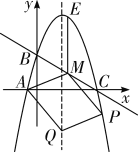 ͼ��
ͼ��
�����ͼ�ܣ���AMΪ�Խ���ʱ���ı���APMQ��ƽ���ı��Σ����ݵ�M����Q��ƽ�ƹ��ɿɵõ�P����A��ƽ�ƹ��ɿ�֪��P�ĺ�����Ϊ![]() ����
����![]() ��
��
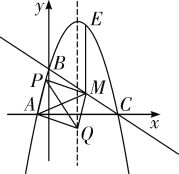 ͼ��
ͼ��
�������������������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ���P��������![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y������x��m��2��m+1��mΪ����������������������ǣ�������
A.��m��2ʱ�����������ֵ�ǩ�1
B.����ͼ��Ķ���ʼ����ֱ��y����x+1��ͼ����
C.����1��x��2ʱ��y��x�������������m��ȡֵ��ΧΪm��2
D.��m��0ʱ������ͼ��Ķ��㼰����ͼ����x����������㹹�ɵ��������ǵ���ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���ACB =90������CAB= 30������ABD�ǵȱ������Σ� ��ͼ2�����ı���ACBD�۵���ʹD��C�غϣ�EFΪ�ۺۣ����ACE������ֵΪ�� ��
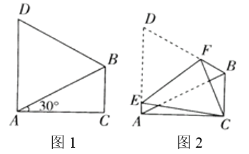
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ��Ʒ��˾��![]() Ԫ�ijɱ��չ���ij��ũ��Ʒ
Ԫ�ijɱ��չ���ij��ũ��Ʒ![]() �֣�Ŀǰ������
�֣�Ŀǰ������![]() Ԫ/�ֵļ۸�ֱ���۳�.���ù�˾������ũ��Ʒ���������ִ�����ʽ�ɹ�ѡ��
Ԫ/�ֵļ۸�ֱ���۳�.���ù�˾������ũ��Ʒ���������ִ�����ʽ�ɹ�ѡ��
��ʽһ����˾�ɽ�����ũ��Ʒֱ����![]() Ԫ/�ֵļ۸��۳���ʣ�µ�ȫ���ӹ��ɰ��Ʒ���ۣ��ӹ��ɱ����Բ��ƣ���ÿ�ָ�ũ��Ʒ���Լӹ��õ�
Ԫ/�ֵļ۸��۳���ʣ�µ�ȫ���ӹ��ɰ��Ʒ���ۣ��ӹ��ɱ����Բ��ƣ���ÿ�ָ�ũ��Ʒ���Լӹ��õ�![]() �ֵİ��Ʒ��ÿ�ְ��Ʒ���ۼ�Ϊ
�ֵİ��Ʒ��ÿ�ְ��Ʒ���ۼ�Ϊ![]() Ԫ.
Ԫ.
��ʽ������˾������ũ��Ʒȫ����������������ÿ���ڻ���ʧ![]() �֣���ÿ������֧�����ַ���
�֣���ÿ������֧�����ַ���![]() Ԫ����ͬʱÿ����ÿ�ֵļ۸�����
Ԫ����ͬʱÿ����ÿ�ֵļ۸�����![]() Ԫ.
Ԫ.
��1�����ù�˾ѡȡ��ʽһ��������ũ��Ʒ�����ջ����![]() �������ʣ���ù�˾ֱ�������˶��ٶ�ũ��Ʒ��
�������ʣ���ù�˾ֱ�������˶��ٶ�ũ��Ʒ��
��2�����ù�˾ѡȡ��ʽ����������ũ��Ʒ�����ջ���1![]() Ԫ�������ũ��Ʒ�����˶��ٸ����ڲų��ۣ�
Ԫ�������ũ��Ʒ�����˶��ٸ����ڲų��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڿ�չ��ʳƷ��ȫ�������������Ϊ�˽�ѧ����ʳƷ��ȫ֪ʶ���˽������ѧУ�����ȡ�˲���ѧ�������ʾ����飬��������������A�dz��˽⡢B�˽⡢C�˽���١�D���˽�������ֱ����ͳ�ƣ�����������������ͳ��ͼ�����������������ͼ����Ϣ������������⣺

��1���˴ι��������� ����ѧ����
��2������ͳ��ͼ��D�������ε�Բ�Ľ�Ϊ�� ����
��3�������������ͳ��ͼ����������
��4������У����800��ѧ����������ƶ�ʳƷ��ȫ֪ʶ���dz��˽�����ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ���κ���
Ϊ���κ���![]() ͼ��Ķ��㣬ֱ��
ͼ��Ķ��㣬ֱ��![]() �ֱ�
�ֱ�![]() ��ĸ������
��ĸ������![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��
(1)�����κ���ͼ����![]() ������κ����Ľ���ʽ��
������κ����Ľ���ʽ��
(2)��ͼ������![]() ����Ϊ
����Ϊ![]() ���ҵ�
���ҵ�![]() ��
��![]() �ڲ�(�������߽�)��
�ڲ�(�������߽�)��
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��
��![]() ���ڶ��κ���ͼ���ϣ��ԱȽ�
���ڶ��κ���ͼ���ϣ��ԱȽ�![]() ��
��![]() �Ĵ�С
�Ĵ�С

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ҹ��Ŀ��������õ��˴���ȵ���ߣ������������ij����1���µĿ�������������������Ľ�����Ƴ����µ�������������ͳ��ͼ��
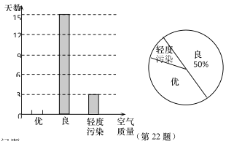
�����ͼ���ṩ����Ϣ�������������⣺
��1�����ε����У�һ�����������Ϊ_______�죻����ͼ�У���ʾ�������Ⱦ�������ε�Բ�Ľ�Ϊ______�ȣ�
��2��������ͼ����������
��3�����Ƹó���һ�꣨��365����㣩�У���������δ�ﵽ�ŵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƶ����С��Թ�ũ���о���ƶ��������ũ��һ���л���̬ˮ���ؿ����г�����ȥ����ȣ���������ˮ���IJ���������1000ǧ�ˣ�ÿǧ�˵�ƽ�������۱�ȥ�꽵����1Ԫ�����������ܶ��ȥ��������![]() ��
��
��1����֪ȥ������ˮ�����������ܶ�Ϊ10��Ԫ��������ˮ������ÿǧ�˵�ƽ���������Ƕ���Ԫ��
��2��ijˮ����ӹ�ũ��ֱ��������רӪ����ˮ�������鷢�֣���ÿǧ�˵�ƽ�����ۼ�Ϊ41Ԫ����ÿ����۳�300ǧ�ˣ���ÿǧ�˵�ƽ�����ۼ�ÿ����3Ԫ��ÿ��ɶ�����180ǧ�ˣ���ˮ����һ�������Ϊ![]() Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����
ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�
��Ŀ | ѧ���������� | �ٷֱ� |
��ɳ�� | 20 | 10% |
������ | 60 | p% |
������ | n | 40% |
����� | 40 | 20% |
����ͼ�����ṩ����Ϣ������������⣺
��1��m= ��n= ��p= ��
��2�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��

��3�����ݳ�����������������Ƹ�У2000��ѧ�����ж�����ѧ����ϲ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com