
【题目】如图,已知直线1经过点A(0,﹣1)与点P(2,3).
(1)求直线1的表达式;
(2)若在y轴上有一点B,使△APB的面积为5,求点B的坐标.
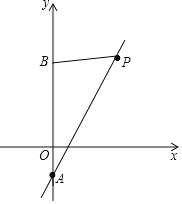
【答案】(1)y=2x﹣1;(2)点B的坐标为(0,4)或(0,﹣6).
【解析】
(1)利用待定系数法求出直线l的表达式即可;
(2)设B(0,m),得出AB的长,由P的横坐标乘以AB长的一半表示出三角形APB面积,由已知面积列方程求出m的值,即可确定出B的坐标.
解:(1)设直线l表达式为y=kx+b(k,b为常数且k≠0),
把A(0,﹣1),P(2,3)代入得:
![]() ,解得:
,解得:![]() ,
,
则直线l表达式为y=2x﹣1;
(2)设点B的坐标为(0,m),则AB=|1+m|,
∵△APB的面积为5,
∴![]() ABxP=5,即
ABxP=5,即![]() |1+m|×2=5,
|1+m|×2=5,
整理得:|1+m|=5,即1+m=5或1+m=﹣5,
解得:m=4或m=﹣6,
故点B的坐标为(0,4)或(0,﹣6).


科目:初中数学 来源: 题型:
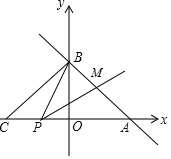
【题目】如图,已知直线y=-![]() x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
(1)求点C的坐标;
(2)设点P为线段CA上的一个动点,点P与点A、C不重合.联结PB.以点P为端点作射线PM交AB于点M,使∠BPM=∠BAC.
①求证:△PBC∽△MPA.
②是否存在点P,使△PBM为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为16,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为16,则k的值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.

(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
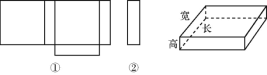
【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数值随自变量增大而增大 B. 函数图像与![]() 轴正方向成45°角
轴正方向成45°角
C. 函数图像不经过第四象限 D. 函数图像与![]() 轴交点坐标是(0,6)
轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
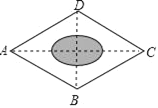
【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个对角线为AC和BD的菱形,使不规则区域落在菱形内,其中AC=8m,BD=4m,现向菱形内随机投掷小石子(假设小石子落在菱形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数25%,由此可估计不规则区域的面积是_____m2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com