
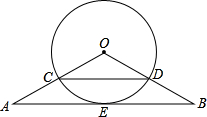
 如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.
如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.分析 (1)根据OC=OD,OA=OB,得到$\frac{OC}{OA}$=$\frac{OD}{OB}$,根据平行线的判定定理证明即可;
(2)连接OE,根据等腰三角形的三线合一得到OE⊥AB,根据题意和直角三角形的性质求出OE、OC的长,根据切线的判定定理证明即可.
解答 证明:(1)∵OC=OD,OA=OB,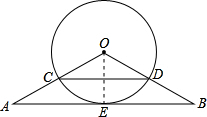
∴$\frac{OC}{OA}$=$\frac{OD}{OB}$,
∴CD∥AB;
(2)连接OE,
∵OA=OB,E是AB的中点,
∴OE⊥AB,又∠A=30°,
∴OE=4,
∵CD∥AB,
∴∠OCD=∠A=30°,
又∵CD=4$\sqrt{3}$,
∴OC=4,
∴OE=OC,
又OE⊥AB,
∴AB是⊙O的切线.
点评 本题考查的是切线的判定定理、平行线的判定定理、直角三角形的性质,切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
| 胜(场) | 平(场) | 负(场) | 积分 | |
| 万达队 | 8 | 2 | 2 | 26 |
| 申花队 | 6 | 5 | 1 | 23 |
| 国安队 | 5 | 7 | 0 | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com