
分析 将三式系数取各系数的最小公倍数,相同因式的次数取最高次幂,即可得出答案.
解答 解:$\frac{1}{4-2x}$=-$\frac{1}{2(x-2)}$=-$\frac{(x-2)(x+2)}{2(x+2)(x-2)^{2}}$,
$\frac{x}{{x}^{2}-4}$=$\frac{2x(x-2)}{2(x+2)(x-2)^{2}}$,
$\frac{3}{{x}^{2}-4x+4}$=$\frac{3}{(x-2)^{2}}$=$\frac{6(x+2)}{2(x+2)(x-2)^{2}}$.
点评 此题考查了通分,解答此题的关键是熟知找公分母的方法:
(1)系数取各系数的最小公倍数;
(2)凡出现的因式都要取;
(3)相同因式的次数取最高次幂.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
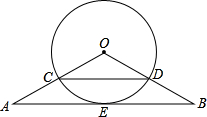 如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.
如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
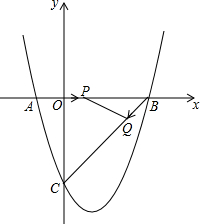 如图,在平面直角坐标系中,抛物线y=ax2-2ax-3与x轴交于A、B,且AB=4,与y轴交于C点,
如图,在平面直角坐标系中,抛物线y=ax2-2ax-3与x轴交于A、B,且AB=4,与y轴交于C点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 行驶里程n(千米) | 每千米q(升)耗油量 | 剩油量A(升) |
| 1 | 0.04 | 20-0.04 |
| 2 | 0.08 | 20-0.08 |
| 3 | 0.12 | 20-0.12 |
| … | …. | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com