
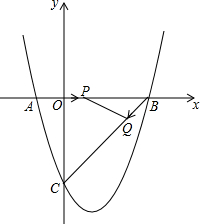
 如图,在平面直角坐标系中,抛物线y=ax2-2ax-3与x轴交于A、B,且AB=4,与y轴交于C点,
如图,在平面直角坐标系中,抛物线y=ax2-2ax-3与x轴交于A、B,且AB=4,与y轴交于C点,分析 (1)先对称轴公式算出对称轴,再根据AB=4,得出A、B两点坐标,将其中一个点的坐标代入解析式即可求出a;
(2)用t表示出PB和PB边上的高,得出面积与t的函数关系式,配方得出最大值;
(3)过点M作ME⊥DE于E,过点N作NF⊥DE于F,根据∠MDE=∠NDE得出△MDE∽△NDE,设出M、N、D三点的坐标(只设横坐标,纵坐标用横坐标表示),分别用横坐标之差、纵坐标之差表示出两个相似三角形的直角边,列出比例等式;设出MN的解析式,与抛物线方程联立,得出两根之和的关系式,结合前面的比例等式解出D点的横坐标,进而算出纵坐标,用两点间的距离公式长出AD、CD的长度,其比值也就自然算出.
解答 解:(1)抛物线y=ax2-2ax-3的对称轴为:x=$-\frac{-2a}{2a}$=1,
∵AB=4,
∴A(-1,0),B(3,0),
将A(-1,0)代入y=ax2-2ax-3解得:a=1,
∴抛物线的解析式为:y=x2-2x-3;
(2)如图1,作QD⊥x轴于点E,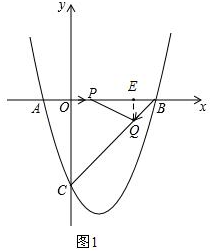
∵OP=3t,OB=3,
∴PB=3-3t,
∵C(0,-3),B(3,0),
∴OB=OC=3,
∴△OCB是等腰直角三角形,
∵QE⊥OB,
∴△QEB也是等腰直角三角形,
∴$EQ=\frac{\sqrt{2}}{2}BQ=\sqrt{2}t$,
∴${S}_{△PBQ}=\frac{1}{2}×PB×EQ$=$-\frac{3\sqrt{2}}{2}{t}^{2}+\frac{3\sqrt{2}}{2}t$=$-\frac{3\sqrt{2}}{2}(t-\frac{1}{2})^{2}+\frac{3\sqrt{2}}{8}$,
∴当t=$\frac{1}{2}$时,△PBQ的最大面积为$\frac{3\sqrt{2}}{8}$;
(3)如图2,过点M作ME⊥DE于E,过点N作NF⊥DE于F,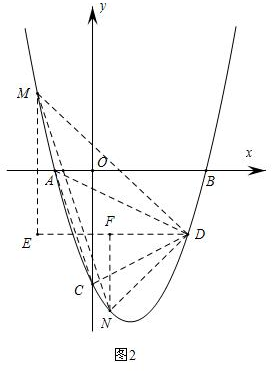
设M(x1,${{x}_{1}}^{2}-2{x}_{1}-3$),N(x2,${{x}_{2}}^{2}-2x-3$),D(x0,${{x}_{0}}^{2}-2{x}_{0}-3$),
则:ME=${{x}_{1}}^{2}-2{x}_{1}-3-{{x}_{0}}^{2}+2{x}_{0}+3$=${{x}_{1}}^{2}-2{x}_{1}-{{x}_{0}}^{2}+2{x}_{0}$=(x1-x0)(x1+x0)-2(x1-x0)=(x1+x0-2)(x1-x0)
DE=x0-x1,
DN=${{x}_{0}}^{2}-2{x}_{0}-3-{{x}_{2}}^{2}+2x+3$=(x0+x2-2)(x0-x1),
DF=x0-x2,
∵∠MDE=∠NDE,
∴△MDE∽△NDE,
∴$\frac{ME}{DE}=\frac{NF}{DF}$,
∴$\frac{({x}_{1}+{x}_{0}-2)({x}_{1}-{x}_{0})}{{x}_{0}-{x}_{1}}$=$\frac{({x}_{0}+{x}_{2}-2)({x}_{0}-{x}_{1})}{{x}_{0}-{x}_{1}}$,
∴${x}_{0}=\frac{-({x}_{1}+{x}_{2})+4}{2}$,
∵A(-1,0),C(0,-3),
∴直线AC的解析式为:y=-3x-3
∵MN∥AC,
∴设直线MN的解析式为y=-3x+b,
由$\left\{\begin{array}{l}{y=-3x+b}\\{y={x}^{2}-2x-3}\end{array}\right.$消去y整理得:x2-x-3-b=0,
由韦达定理可知:x1+x2=1,
∴${x}_{0}=\frac{3}{2}$,
∴${{x}_{0}}^{2}-2{x}_{0}-3=-\frac{15}{4}$,
∴D($\frac{3}{2}$,$-\frac{15}{4}$),
∴AD=$\sqrt{(-1-\frac{3}{2})^{2}+(0+\frac{15}{4})^{2}}$=$\frac{5\sqrt{13}}{4}$,
∴CD=$\sqrt{(0-\frac{3}{2})^{2}+(-3+\frac{15}{4})^{2}}$=$\frac{3\sqrt{5}}{4}$,
∴$\frac{AD}{CD}=\frac{\sqrt{65}}{3}$.
点评 本题是二次函数的综合题,主要考查了待定系数法求抛物线解析式、抛物线的对称性、相似三角形的判定与性质、等腰直角三角形的性质、三角形面积计算、配方法求二次函数最值、角平分线的定义、两点间的距离公式、韦达定理等众多知识点,综合性很强,难度较大.本题第(3)问使用代数手段解决几何问题,是几何与代数的巧妙结合,有很强的解析性质,是难点所在,熟练掌握这些技巧,对今后高中的数学学习有很大的帮助.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
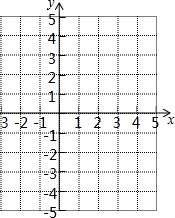 已知在平面直角坐标系中点A(-2,-2),B(1,-2),C(3,2),D(0,2)按照下列要求作图:
已知在平面直角坐标系中点A(-2,-2),B(1,-2),C(3,2),D(0,2)按照下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB∥CD且AB=CD | B. | AB=AD、BC=CD | C. | AB=CD,AD=BC | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com