
【题目】如图,在△ABC中,已知∠ABC=120°,AC=4,

(1)用直尺和圆规作出△ABC的外接圆⊙O(不写作法,保留作图痕迹);
(2)求∠AOC的度数;
(3)求⊙O的半径.
【答案】(1)见解析 (2)120°; (3)![]() .
.
【解析】(1)分别作线段AB于BC的垂直平分线相交于点O,以点O为圆心,OA的长为半径画圆即可;
(2)在优弧AC上取点P,连接AP,PC,利用圆内接四边形的性质求出∠P的度数,再由圆周角定理即可得出∠AOC的度数;
(3)过点O作OD⊥AC于点D,利用垂径定理得出AD的长,根据直角三角形的性质即可得出OA的长.
解:(1)如图,⊙O即为所求;
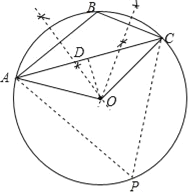
(2)在优弧AC上取点P,连接AP,PC,
∵∠ABC=120°,
∴∠P=180°﹣120°=60°,
∴∠AOC=2∠P=120°;
(3)过点O作OD⊥AC于点D,
∵AC=4,
∴AD=![]() AC=2.
AC=2.
∵∠AOC=120°,OA=OC.
∴∠OAC=![]() =30°,
=30°,
∴OA=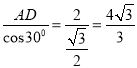 .
.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到 ![]() ,再作
,再作 ![]() 关于x轴对称的图形
关于x轴对称的图形 ![]() ,则顶点
,则顶点 ![]() 的坐标是( )
的坐标是( )
A.(-3,-2)
B.(2,-3)
C.(-2,3)
D.(-2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC.△ABC为所求作的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是( )
A.(1)
B.(2)
C.(3)
D.(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com