
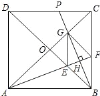
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)试判断四边形BEGF的形状并说明理由.
(2)求![]() 的值.
的值.
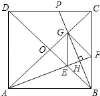
【答案】(1)四边形BEGF是菱形;(2)1+![]() .
.
【解析】
(1)先证明△AHG≌△AHB,得出GH=BH,由线段垂直平分线的性质得出EG=EB,FG=FB;再证出∠BEF=∠BFE,得出EB=FB,因此EG=EB=FB=FG,即可得出结论;
(2)设OA=OB=OC=a,菱形BEGF的边长为b,由菱形的性质CG=GF=b,(也可由△OAE≌△OBG得OG=OE=a﹣b,OC﹣CG=a﹣b,得CG=b);然后在Rt△GOE中,由勾股定理可得a和b的关系,通过相似三角形△CGP∽△AGB的对应边成比例得到:![]() ,即可得到答案.
,即可得到答案.
(1)四边形BEGF是菱形.理由如下:
∵∠GAH=∠BAH,AH=AH,∠AHG=∠AHB=90°,∴△AHG≌△AHB,∴GH=BH,∴AF是线段BG的垂直平分线,∴EG=EB,FG=FB.
∵∠BEF=∠BAF+∠ABE=67.5°,∠BFE=90°﹣∠BAF=67.5°,∴∠BEF=∠BFE,∴EB=FB,∴EG=EB=FB=FG,∴四边形BEGF是菱形.
(2)设OA=OB=OC=a,菱形BEGF的边长为b.
∵四边形BEGF是菱形,∴GF∥OB,∴∠CGF=∠COB=90°,∴∠GFC=∠GCF=45°,∴CG=GF=b.
∵四边形ABCD是正方形,∴OA=OB,∠AOE=∠BOG=90°
∵BH⊥AF,∴∠GAH+∠AGH=90°=∠OBG+∠AGH,∴∠GAH=∠OBG,∴△OAE≌△OBG,∴OG=OE=a﹣b,AE=BG.
∵在Rt△GOE中,GE![]() OG,∴b
OG,∴b![]() (a﹣b),整理得:a
(a﹣b),整理得:a![]() b,∴AC=2a=(2
b,∴AC=2a=(2![]() )b,AG=AC﹣CG=(1
)b,AG=AC﹣CG=(1![]() )b.
)b.
∵PC∥AB,∴△ABG∽△CPG,∴![]() ,∴
,∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
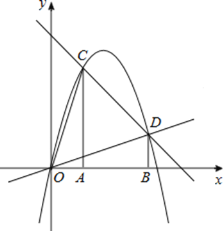
【题目】如图,过![]() 、
、![]() 作x轴的垂线,分别交直线
作x轴的垂线,分别交直线![]() 于C、D两点
于C、D两点![]() 抛物线
抛物线![]() 经过O、C、D三点.
经过O、C、D三点.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
![]() 若
若![]() 沿CD方向平移
沿CD方向平移![]() 点C在线段CD上,且不与点D重合
点C在线段CD上,且不与点D重合![]() ,在平移的过程中
,在平移的过程中![]() 与
与![]() 重叠部分的面积记为S,试求S的最大值.
重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围.
(2)是否存在实数k,使得x1x2﹣x12﹣x22=﹣16成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
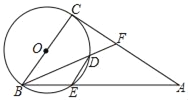
【题目】如图,以BC为直径的⊙O交的边AB于E,点D在⊙O上,且DE∥BC,连BD并延长交CA于F,∠CBF=∠A.
(1)求证:CA是⊙O的切线;
(2)若⊙O的半径为2,BD=2BE,则DE长为 (直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “打开电视机,正在播世界杯足球赛”是必然事件
B. “掷一枚硬币正面朝上的概率是![]() ”表示每抛掷硬币2次就有1次正面朝上
”表示每抛掷硬币2次就有1次正面朝上
C. 一组数据2,3,4,5,5,6的众数和中位数都是5
D. 甲组数据的方差S甲2=0.09,乙组数据的方差S乙2=0.56,则甲组数据比乙组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
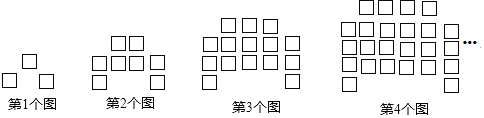
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
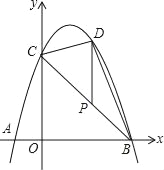
【题目】如图,抛物线y=﹣x2+bx+c经过点A,B,C,已知点A(﹣1,0),点C(0,3).
(1)求抛物线的表达式;
(2)P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)设E是抛物线上的一点,在x轴上是否存在点F,使得A,C,E,F为顶点的四边形是平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
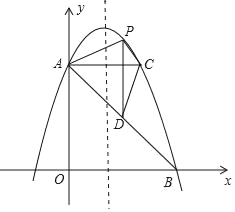
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与y轴交于点A,与x轴交于点B.抛物线y=﹣x2+bx+c过A、B两点.
(1)点A,B的坐标分别是A ,B ;
(2)求抛物线的解析式;
(3)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一动点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com