
【题目】如图①,在等腰![]() 中,如图①,在等腰
中,如图①,在等腰![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .点
.点![]() 为线段
为线段![]() 上一点(不与端点
上一点(不与端点![]() 、
、![]() 重合),
重合),![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
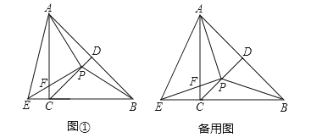
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)探究线段![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)证明见解析;(2)∠EAP=45°;(3)EC=![]() PD.
PD.
【解析】
(1)根据等腰直角三角形的性质可得CD是AB的垂直平分线,根据垂直平分线的性质可得AP=BP;
(2)由∠ACE=∠APE=90°,可得点A,点P,点C,点E四点共圆,可得∠AEP=∠ACD=45°,即可求∠EAP的度数;
(3)过点E作EH⊥CD于点H,根据“AAS”可证△APD≌△PEH,可得EH=PD,根据勾股定理可求EC=![]() EH,即可得EC=
EH,即可得EC=![]() PD.
PD.
证明:(1)∵∠ACB=90°,AC=BC,CD平分∠ACB,
∴CD⊥AB,AD=BD,∠ACD=∠BCD=∠CAD=∠DBC=45°,
∴CD是AB的垂直平分线
∴AP=BP,
(2)∵∠ACE=∠APE=90°,
∴点A,点P,点C,点E四点共圆,
∴∠AEP=∠ACD=45°,且AP⊥EP,
∴∠EAP=45°
(3)EC=![]() PD,理由如下:
PD,理由如下:
如图,过点E作EH⊥CD于点H,
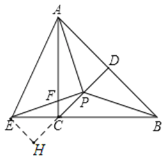
∵∠EAP=∠AEP=45°,
∴AP=PE,
∵∠APE=90°=∠ADP
∴∠APD+∠PAD=90°,∠APD+∠EPH=90°,
∴∠PAD=∠EPH,且AP=PE,∠EHP=∠ADP=90°
∴△APD≌△PEH(AAS)
∴EH=PD,
∵∠ECH=∠DCB=45°,EH⊥CD
∴∠HEC=∠HCE=45°
∴EH=CH
在Rt△ECH中![]()
∴EC=![]() PD.
PD.


科目:初中数学 来源: 题型:
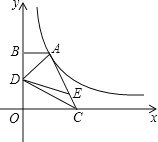
【题目】如图,点A在双曲线y=![]() (k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
(k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受疫情的影响,很多农产品滞销,各大电商发起了“爱心助农”活动,帮助农户进行农产品销售.已知某种橘子的成本为4元/千克,经过市场调查发现,一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示:

(1)当4≤x≤8时,求y与x的函数解析式;
(2)当4≤x≤8时,要使一天内获得的利润为1200元,单价应定为多少?
(3)求橘子的单价定为多少时,一天内获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C = 90°, P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,设PC的长度为xcm,BQ的长度为ycm .

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1) 按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x ,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y > 2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
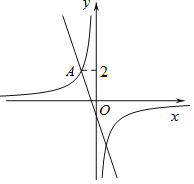
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数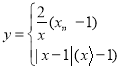 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
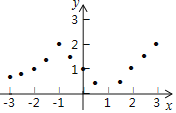
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下图:
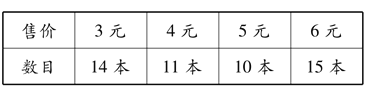
下列说法正确的是( )
A.该班级所售图书的总数收入是226元
B.在该班级所售图书价格组成的一组数据中,中位数是4
C.在该班级所售图书价格组成的一组数据中,众数是15
D.在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com