
【题目】如图,在梯形ABCD中,![]() ,AD=BC,E是CD的中点,BE交AC于F,过点F作
,AD=BC,E是CD的中点,BE交AC于F,过点F作![]() ,交AE于点G.
,交AE于点G.
(1)求证:AG=BF;
(2)当![]() 时,求证:
时,求证:![]() .
.
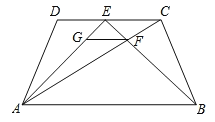
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等腰梯形的性质求得∠ADE=∠BCE,进而证得△ADE≌△BCE,得出AE=BE,根据平行线分线段成比例定理即可证得结论;
(2)先根据已知条件证得△CAB∽△CBF,证得![]() ,因为BF=AG,BC=AD,所以
,因为BF=AG,BC=AD,所以![]() ,从而证得ABAD=AGAC.
,从而证得ABAD=AGAC.
证明:(1)∵在梯形ABCD中,AB∥CD,AD=BC,
∴∠ADE=∠BCE,
在△ADE和△BCE中
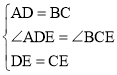
∴△ADE≌△BCE.
∴AE=BE,
∵FG∥AB,
∴![]() ,
,
∴AG=BF.
(2)∵AD2=CACF,
∴![]() ,
,
∵AD=BC,
∴![]() .
.
∵∠BCF=∠ACB,
∴△CAB∽△CBF.
∴![]() .
.
∵BF=AG,BC=AD,
∴![]() .
.
∴ABAD=AGAC.


科目:初中数学 来源: 题型:
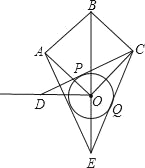
【题目】如图所示,在边长为4![]() 正方形OABC中,OB为对角线,过点O作OB的垂线.以点O为圆心,r为半径作圆,过点C做⊙O的两条切线分别交OB垂线、BO延长线于点D、E,CD、CE分别切⊙O于点P、Q,连接AE.
正方形OABC中,OB为对角线,过点O作OB的垂线.以点O为圆心,r为半径作圆,过点C做⊙O的两条切线分别交OB垂线、BO延长线于点D、E,CD、CE分别切⊙O于点P、Q,连接AE.
(1)请先在一个等腰直角三角形内探究tan22.5°的值;
(2)求证:
①DO=OE;
②AE=CD,且AE⊥CD.
(3)当OA=OD时:
①求∠AEC的度数;
②求r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
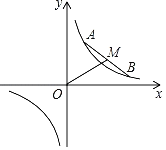
【题目】如图,在平面直角坐标系中.点A、B在反比例函数y=![]() 的图象上运动,且始终保持线段AB=4
的图象上运动,且始终保持线段AB=4![]() 的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
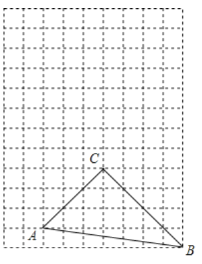
【题目】如图,在每个边长为1的小正方形的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 是
是![]() 边上任意一点,以
边上任意一点,以![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把点
,把点![]() 逆时针旋转,点
逆时针旋转,点![]() 的对应点为
的对应点为![]() ,当
,当![]() 最短时,画出点
最短时,画出点![]() ,并说明
,并说明![]() 最短的理由是________.
最短的理由是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在等腰![]() 中,如图①,在等腰
中,如图①,在等腰![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .点
.点![]() 为线段
为线段![]() 上一点(不与端点
上一点(不与端点![]() 、
、![]() 重合),
重合),![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
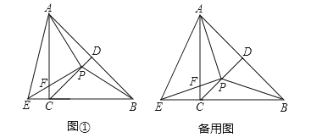
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)探究线段![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(![]() ,4),B(3,m)是直线AB与反比例函数
,4),B(3,m)是直线AB与反比例函数![]() (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
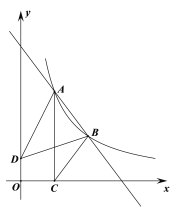
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是()
A.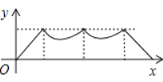 B.
B.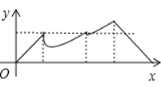 C.
C.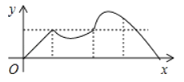 D.
D.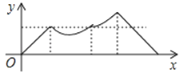
查看答案和解析>>
科目:初中数学 来源: 题型:
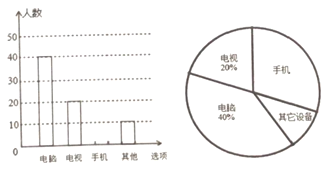
【题目】受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它”四种类型的设备对学生做了一次抽样调查.调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有1500名学生,估计全校用手机上网课的学生共有___________名;
(3)在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com