
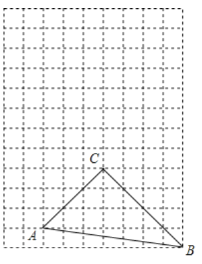
【题目】如图,在每个边长为1的小正方形的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 是
是![]() 边上任意一点,以
边上任意一点,以![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把点
,把点![]() 逆时针旋转,点
逆时针旋转,点![]() 的对应点为
的对应点为![]() ,当
,当![]() 最短时,画出点
最短时,画出点![]() ,并说明
,并说明![]() 最短的理由是________.
最短的理由是________.
【答案】垂线段最短
【解析】
连CF,根据已知条件得到A、C、F共线,求得AF=5![]() =AB,根据相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到结论.
=AB,根据相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到结论.
解:作图过程如下:
取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求
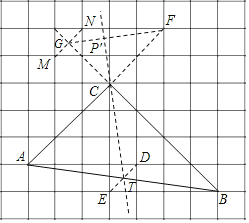
理由:连CF,
∵AC,CF为正方形网格对角线
∴A、C、F共线
∴AF=5![]() =AB,
=AB,
由图形可知:GC=![]() ,CF=2
,CF=2![]() ,
,
∵AC=![]() ,BC=4
,BC=4![]() ,
,
∴△ACB∽△GCF,
∴∠GFC=∠B,
∵AF=5![]() =AB,
=AB,
∴当BC边绕点A逆时针旋转∠CAB时,点B与点F重合,点C在射线FG上.
由作图可知T为AB中点,
∴∠TCA=∠TAC,
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°,
∴CP′⊥GF,
此时,CP′最短,
故答案为:垂线段最短.


科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,提出圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得圆周率π的近似值.如图,设半径为r的内接正n边形的周长为C,圆的直径为d,则π≈![]() .例如,当n=6时,π
.例如,当n=6时,π![]() ,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
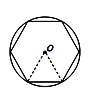
A.3.11B.3.12C.3.13D.3.14
查看答案和解析>>
科目:初中数学 来源: 题型:
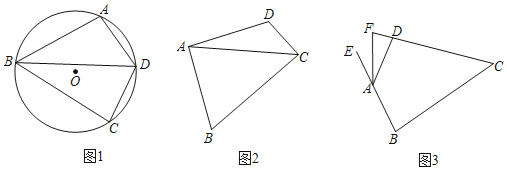
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
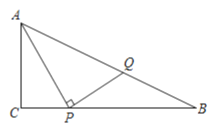
【题目】如图,Rt△ABC中,∠C = 90°, P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,设PC的长度为xcm,BQ的长度为ycm .

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1) 按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x ,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y > 2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() 交
交![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() .
.
小青同学根据学习函数的经验对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 的几组对应值:
的几组对应值:
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
| 0 | 1.56 | 2.24 | 2.51 |
| 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时相关数据保留一位小数)
![]() 的值约为__________
的值约为__________![]() ;
;
(2)在平面直角坐标系中,描出已补全后的表格中各组数值所对应的点![]() ,画出该函数的图象;
,画出该函数的图象;
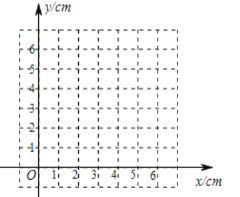
(3)结合画出的函数图象,解决问题:
①当![]() 时,对应的
时,对应的![]() 的取值范围约是_____________;
的取值范围约是_____________;
②若点![]() 不与
不与![]() ,
,![]() 两点重合,是否存在点
两点重合,是否存在点![]() ,使得
,使得![]() ?________________(填“存在”或“不存在”)
?________________(填“存在”或“不存在”)
查看答案和解析>>
科目:初中数学 来源: 题型:
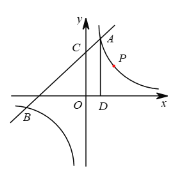
【题目】如图,一次函数y1=k1x+4与反比例函y2=![]() 的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.
的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.
⑴k1= ,k2= ;
⑵根据函数图象知,当y1>y2时,x的取值范国是 ;
⑶过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点,设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=4:1时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() 过
过![]() 其中一个顶点的直线把
其中一个顶点的直线把![]() 分成两个等腰三角形.
分成两个等腰三角形.
(1)如图1,若![]() 求
求![]() 的值;
的值;

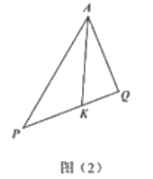
(2)![]() 度(
度(![]() 除外) ;
除外) ;
(3)如图2,![]() 为锐角,
为锐角,![]() 在
在![]() 延长线上,
延长线上,![]() 在边
在边![]() 上,
上,![]() 平分
平分![]() 交
交![]() 于
于![]() 请求线段
请求线段![]()
![]() 三者之者的数量关系. (用
三者之者的数量关系. (用![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com