
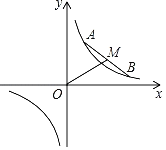
【题目】如图,在平面直角坐标系中.点A、B在反比例函数y=![]() 的图象上运动,且始终保持线段AB=4
的图象上运动,且始终保持线段AB=4![]() 的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
【答案】![]() .
.
【解析】
如图,当OM⊥AB时,线段OM长度的最小.首先证明点A与点B关于直线y=x对称,因为点A,B在反比例函数y=![]() (k≠0)的图象上,AB=
(k≠0)的图象上,AB=![]() ,所以可以假设A(m,
,所以可以假设A(m,![]() ),则B(m+4,
),则B(m+4,![]() ﹣4),则(m+4)(
﹣4),则(m+4)(![]() ﹣4)=5,整理得5=m2+4m,推出A(1,5),B(5,1),可得M(3,3),求出OM即可解决问题.
﹣4)=5,整理得5=m2+4m,推出A(1,5),B(5,1),可得M(3,3),求出OM即可解决问题.
如图,因为反比例函数关于直线y=x对称,观察图象可知:当线段AB与直线y=x垂直时,垂足为M,此时AM=BM,OM的值最小,
∵M为线段AB的中点,
∴OA=OB,
∵点A,B在反比例函数y=![]() 的图象上,
的图象上,
∴点A与点B关于直线y=x对称,
∵AB=![]() ,
,
∴可以假设A(m,![]() ),则B(m+4,
),则B(m+4,![]() ﹣4),
﹣4),
∴(m+4)(![]() ﹣4)=5,
﹣4)=5,
整理得5=m2+4m,
解得:m=1(负值舍去),
∴A(1,5),B(5,1),
∴M(3,3),
∴OM=![]() ,
,
∴线段OM的长度为![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读![]() 本书籍的人数所在扇形的圆心角度数是 ;
本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有![]() 名学生,估计该校在这次活动中阅读书籍的数量不低于
名学生,估计该校在这次活动中阅读书籍的数量不低于![]() 本的学生有多少人?
本的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,提出圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得圆周率π的近似值.如图,设半径为r的内接正n边形的周长为C,圆的直径为d,则π≈![]() .例如,当n=6时,π
.例如,当n=6时,π![]() ,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
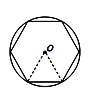
A.3.11B.3.12C.3.13D.3.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受疫情的影响,很多农产品滞销,各大电商发起了“爱心助农”活动,帮助农户进行农产品销售.已知某种橘子的成本为4元/千克,经过市场调查发现,一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示:

(1)当4≤x≤8时,求y与x的函数解析式;
(2)当4≤x≤8时,要使一天内获得的利润为1200元,单价应定为多少?
(3)求橘子的单价定为多少时,一天内获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
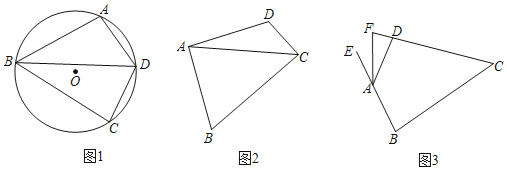
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C = 90°, P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,设PC的长度为xcm,BQ的长度为ycm .

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1) 按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x ,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y > 2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从A地出发,匀速开往B地,甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动:当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h,设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.

(1)A、B两地的距离是 km,乙车的速度是 km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距50km时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com