
【题目】甲、乙两车同时从A地出发,匀速开往B地,甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动:当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h,设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.

(1)A、B两地的距离是 km,乙车的速度是 km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距50km时,直接写出x的值.
【答案】(1)600,75;(2)y=-225x+1200;(3)当两车相距50km时,x的值是![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据题意和函数图象中的数据,可知A、B两地的距离是150×4=600km,然后根据当甲车到达A地时,乙车恰好到达B地,可以得到乙车的速度;
(2)根据题意,可以求得点M的坐标,然后即可写出点M表示的实际意义,再根据函数图象中的数据,可以求得线段MN所表示的y与x之间的函数表达式;
(3)根据题意和函数图象中的数据,可以求得当两车相距50km时,对应的x的值.
(1)由图象可得,
A、B两地的距离是150×4=600(km),
乙车的速度为:150÷2=75(km/h),
故答案为:600,75;
(2)600÷150=4小时
(150-75)×4=75×4=300(km),
点M的实际意义是,在两车行驶4小时时,甲车到达B地,此时甲乙两车的距离是300km,
即点M的坐标为(4,300),
点N的横坐标为:600×2÷(150+75)=![]() ,
,
即点N的坐标为(![]() ,0),
,0),
设线段MN所表示的y与x之间的函数表达式为y=kx+b,
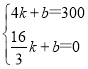 ,得
,得![]() ,
,
即线段MN所表示的y与x之间的函数表达式为y=-225x+1200;
(3)当0≤x≤4时,
(150-75)x=50,
解得x=![]() ;
;
当4<x≤![]() 时,
时,
(150+75)x+50=600×2,
解得,x=![]() ;
;
当x>![]() 时,
时,
(150+75)x-50=600×2,
解得,x=![]() ;
;
由上可得,当两车相距50km时,x的值是![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
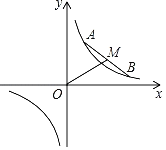
【题目】如图,在平面直角坐标系中.点A、B在反比例函数y=![]() 的图象上运动,且始终保持线段AB=4
的图象上运动,且始终保持线段AB=4![]() 的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
的长度不变,M为线段AB的中点,连接OM,则线段OM的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
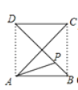
【题目】如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是()
A. B.
B.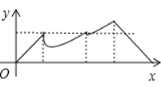 C.
C.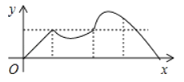 D.
D.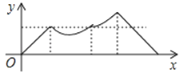
查看答案和解析>>
科目:初中数学 来源: 题型:
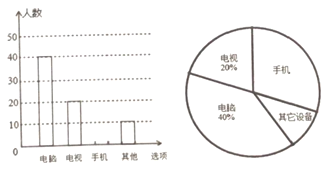
【题目】受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它”四种类型的设备对学生做了一次抽样调查.调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有1500名学生,估计全校用手机上网课的学生共有___________名;
(3)在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )

A.70°B.60°C.40°D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:①abc<0;②b2﹣4ac<0;③2a+b>0;④a﹣b+c<0,其中正确的个数( )
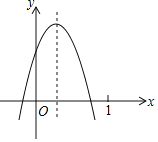
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,可得到△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1,则△AnCnCn+1的周长为_______(n≥1,且n为整数).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com