
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数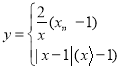 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
科目:初中数学 来源: 题型:
【题目】随着网络购物的盛行,“菜鸟驿站”新兴的代收快递业务越来越受到人们的青睐.“菜鸟驿站”某代收点只代收![]() ,
,![]() 两区的快递.4月份该代收点对
两区的快递.4月份该代收点对![]() ,
,![]() 两区代收数据进行统计,
两区代收数据进行统计,![]() 区比
区比![]() 区平均每个快递轻1千克.
区平均每个快递轻1千克.
(1)4月份第四周![]() 区共有300个快递,
区共有300个快递,![]() 区快递数为
区快递数为![]() 区的
区的![]() ,若本周该代收点的快递重量不低于1700千克,则
,若本周该代收点的快递重量不低于1700千克,则![]() 区该周平均每个快递至少重多少千克?
区该周平均每个快递至少重多少千克?
(2)随着夏季的到来,5月份第四周![]() 区快递数比4月份第四周增长了
区快递数比4月份第四周增长了![]() ,但
,但![]() 区平均每个快递比(1)中相应最少重量减少了
区平均每个快递比(1)中相应最少重量减少了![]() 千克,
千克,![]() 区快递数比4月份第四周增长了10%,平均每单比(1)中相应最少重量减少了
区快递数比4月份第四周增长了10%,平均每单比(1)中相应最少重量减少了![]() ,第四周两区快递总重量比第四周的最少重量减少了336千克,求
,第四周两区快递总重量比第四周的最少重量减少了336千克,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
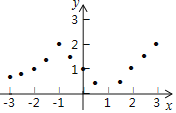
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 是常数),其图象与水平直线
是常数),其图象与水平直线![]() ,
,![]() ,铅直直线
,铅直直线![]() ,
,![]() 的位置如图所示,若以其中的两条直线为
的位置如图所示,若以其中的两条直线为![]() 轴,
轴,![]() 轴所在的直线建立平面直角坐标系(向右为
轴所在的直线建立平面直角坐标系(向右为![]() 轴正方向,向上为
轴正方向,向上为![]() 轴正方向),则下列说法正确的是( )
轴正方向),则下列说法正确的是( )

A.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]() B.
B.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]()
C.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]() D.
D.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
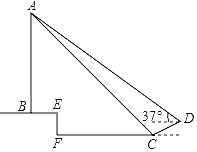
A.10.2B.9.8C.11.2D.10.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.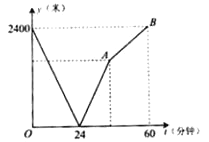
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
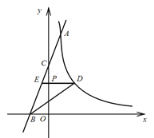
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)在![]() 轴上有一动点
轴上有一动点![]()
![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交反比例函数的图像于点
轴的直线,交反比例函数的图像于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com