
【题目】如图,在平面直角坐标系中,已知抛物线y=a(x-5)(x+1)与x轴交于点A,B两点,与y轴交于点C(0,![]() ).
).
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF.当线段EF的长度最短时,求出点G的坐标.

【答案】(1)![]() ;(2)P(-5,-20);(3)G(
;(2)P(-5,-20);(3)G(![]() ,2) (
,2) (![]() ,2)
,2)
【解析】试题分析:(1)运用待定系数法即可求出抛物线的解析式;
(2)过点A作![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线与点
,交抛物线与点![]() ,通过
,通过![]() ∽
∽![]() 求得OH的长,从而得到H点坐标,继而得到直线AP的解析式,与抛物线解析式联立即可得到点P坐标;
求得OH的长,从而得到H点坐标,继而得到直线AP的解析式,与抛物线解析式联立即可得到点P坐标;
(3)连接OD,易得四边形OFDE是矩形,则OD=EF,根据垂线段最短可得当![]() 时,OD(即EF)的长度最小.然后只需求出点D的纵坐标,就可得到点G的纵坐标,代入解析式就可求出点G的横坐标,从而得到点G的坐标.
时,OD(即EF)的长度最小.然后只需求出点D的纵坐标,就可得到点G的纵坐标,代入解析式就可求出点G的横坐标,从而得到点G的坐标.
(1) ∵抛物线![]() 与
与![]() 轴交于点C(0,
轴交于点C(0, ![]() ),∴
),∴![]() ,
,
∴![]() ;
;
(2)过点A作![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线与点
,交抛物线与点![]() ,则A(5,0),B(-1,0)
,则A(5,0),B(-1,0)
∵![]() ,
, ![]()
∴![]() ∽
∽![]() span> ∴
span> ∴![]() ∴
∴![]() ;
;
又∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴H(0,-10),A(5,0),∴直线AP的解析式为y=2x-10![]() ,
,
联立 ∴P(-5,-20);
∴P(-5,-20);
(3)∵![]() 轴,
轴, ![]() 轴,∴四边形OFDE是矩形,∴EF=OD,
轴,∴四边形OFDE是矩形,∴EF=OD,
∴EF长度的最小值为OD长度的最小值,当![]() 时,OD的长度最小.
时,OD的长度最小.
此时![]() ,
, ![]() ,
, ![]()
又∵![]() 轴,
轴, ![]() ,∴
,∴![]() ∽
∽![]() ,∴
,∴![]()
∴![]() ,∴OE=2,∴点G的纵坐标为2,
,∴OE=2,∴点G的纵坐标为2,
∴![]() 解得
解得![]() ,
, ![]()
∴G(![]() ,2) (
,2) (![]() ,2).
,2).



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象经过点(1,2),点(﹣1,6),且与x轴交于点B,与y轴交于点A. 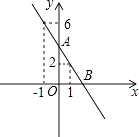
(1)求出这个一次函数的解析式;
(2)求出一次函数图象与两坐标轴围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
“最喜欢的文体活动”调查统计表
项目 | A音乐 | B绘画 | C田径 | D球类 | E其他 |
频数 | 正正正正正正 | ||||
人数(人) | 20 |
(1)根据统计表和图中的信息将“统计表”填写完整;
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
A.本次抽查活动共抽查了2100名学生
B.本次抽查活动中视力不低于4.8的学生人数占总人数的66.7%
C.本次抽查活动中视力不低于4.8学生人数中的极差为300人
D.由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com