
分析 (1)(2)(3)由题意可知:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;
(4)由上面的数字得出n条直线最多有1+2+3+4+…+n-1=$\frac{1}{2}$n(n-1)个交点,进一步代入求得答案即可.
解答 解:如图,
(1)任意画2条直线,它们最多有1个交点;
(2)任意画3条直线,它们最多有3个交点;
(3)任意画4条直线(只画交点个数最多的情况),最多有6个交点;
(4)5条直线最多有10个交点;n条直线最多有$\frac{1}{2}$n(n-1)个交点.
故答案为:1,3,6,10,$\frac{1}{2}$n(n-1).
点评 此题考查图形的变化规律,要从简单的情况着手,仔细观察,得到启示,大胆猜想,找出一般规律解决问题.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
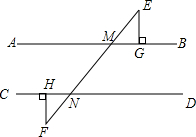 如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.
如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知数轴上有A,B,C三个点,它们表示的数分别是-24,-10,50.动点P,Q在数轴上运动,P,Q的运动速度分别是每秒3个单位长度和每秒4个单位长度.
如图,已知数轴上有A,B,C三个点,它们表示的数分别是-24,-10,50.动点P,Q在数轴上运动,P,Q的运动速度分别是每秒3个单位长度和每秒4个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com