
分析 (1)先估算$\sqrt{5}$的范围,求出x、y的值,再代入求出即可;
(2)把x、y的值代入求出即可.
解答 解:∵2$<\sqrt{5}$<3,x为$\sqrt{5}$的小数部分的倒数,
∴x=$\frac{1}{2}$,
∵xy=1,
∴y=2,
(1)当x=$\frac{1}{2}$,y=2时,
x2-3xy+y2
=($\frac{1}{2}$)2-3×$\frac{1}{2}×2$+22
=1$\frac{1}{4}$;
(2)当x=$\frac{1}{2}$,y=2时,
$\frac{x-y}{{x}^{2}y+x{y}^{2}}$
=$\frac{\frac{1}{2}-2}{(\frac{1}{2})^{2}×2+\frac{1}{2}×{2}^{2}}$
=-$\frac{3}{5}$.
点评 本题考查了估算无理数的大小,倒数,求代数式的值的应用,能求出x、y的值是解此题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
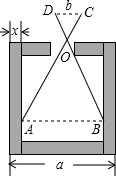 如图,已知零件的外径为a,现用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB,如果OA:OC=OB:OD=n.且量得CD=b.求AB以及零件厚度x.
如图,已知零件的外径为a,现用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB,如果OA:OC=OB:OD=n.且量得CD=b.求AB以及零件厚度x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com