
����Ŀ��Ϊ��Ԥ���¹ڷ��ף�ijҩ�����ۼס������ַ������֣���֪����ÿ�����ۼ۱��ҿ��ֶ�5Ԫ��С���Ӹ�ҩ�깺����3�����ֺ�2���ҿ��ֹ�����115Ԫ��
��1�����ҩ��ס������ֿ���ÿ�����ۼ۷ֱ�Ϊ����Ԫ��
��2����������������ҩ������ò�����8000Ԫ�����ס������ֿ��ֹ�400������֪����ÿ���Ľ���Ϊ22.2Ԫ���ҿ���ÿ���Ľ���Ϊ17.8Ԫ��Ҫʹҩ��������Ӧ�ù����ס������ֿ��ָ����ٴ���������������
���𰸡���1����ҩ�����ÿ�����ۼ�Ϊ25Ԫ���ҿ���ÿ�����ۼ�Ϊ20Ԫ����2��ʹҩ��������ķ����ǹ����ס������ֿ��ָ�200�����ɻ�ȡ���������Ϊ1000Ԫ��
��������
��1����õ���ֿ���ÿ�����ۼ�ΪxԪ�����ֿ���ÿ�����ۼ�ΪyԪ�����ݡ����ֿ���ÿ�����ۼ۱����ֿ��ֶ�5Ԫ��С���Ӹ���������3�����ֿ��ֺ�2�����ֿ��ֹ�����115Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2����ҩ�깺������m����������ΪwԪ����������õ�w��m�ĺ�����ϵʽ����������õ�m��ȡֵ��Χ�������ݺ�����������ȷ��������ɣ�
�⣺��1�����ҩ�����ÿ�����ۼ�ΪxԪ���ҿ���ÿ�����ۼ�ΪyԪ��
���������![]() �����
�����![]() ��
��
�𣺸�ҩ�����ÿ�����ۼ�Ϊ25Ԫ���ҿ���ÿ�����ۼ�Ϊ20Ԫ��
��2�����ҩ�깺������m�������ҿ���![]() ����
����
�������⣬��![]() ��
��
��ã�![]() ��
��
��ҩ�깺���ס������ֿ��ֻ���wԪ��
��![]() ��
��
k=0.6��0��
![]() ��m�����������
��m�����������
![]() ��
��![]() ʱ��w�����ֵ�����ֵΪ
ʱ��w�����ֵ�����ֵΪ![]() ��
��
ʹҩ��������ķ����ǹ����ס������ֿ��ָ�200�����ɻ�ȡ���������Ϊ1000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ�������п���ijУ�ţ�1�����������ʦ��ȫ��45��ѧ��������һ������ģ�����(�÷־�Ϊ����)���ɼ�����Ϊ10�֣��ð������ίԱ������β��Գɼ���������ͳ��ͼ�ͷ��������£�
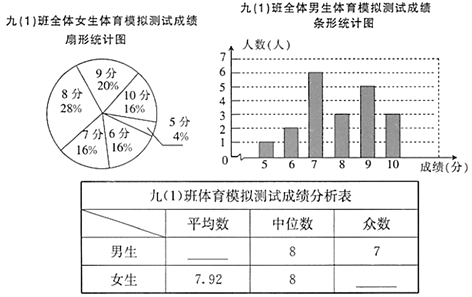
����������Ϣ������������⣮
��1������������_________�ˣ�Ů����____________�ˣ�
��2�����㲹ȫ��(1)������ģ����Գɼ���������
��3������Ϊ���������ģ������У��ţ�1�����ȫ��������ȫ��Ů����˭�ı��ָ���һЩ����д��һ��֧����Ŀ��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ˮ���ӵĺ����Ϊ�ı���ABCD������AD��BC���Ӷ�BC=10�ף��Ӹ�20�ף�б��AB���¶�i=1��2.5��б��CD���½�Ϊ30�㣮
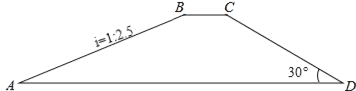
��1����ӵ�AD�ij��ȣ������ȷ��1�ף���
��2�����ӳ�100�ף�������������Ҫ����ʯ�ϣ��ο����ݣ� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�涨max��a��b����![]() �����磺max����1��2����2��max��3��3����3��
�����磺max����1��2����2��max��3��3����3��
��֪����֪����y��max��x+1����2x+4��
��1����x��3ʱ��y��_____��
��2����y��3ʱ��x��______��
��3����y��x�����������ʱ��x��ȡֵ��ΧΪ______��
��4������1��x��4ʱ��y��ȡֵ��ΧΪ______��
̽������֪����y��max��x+2��![]() ����ֱ��y��m��mΪ�������뺯��y��max��x+2��
����ֱ��y��m��mΪ�������뺯��y��max��x+2��![]() ������6��x��3����ͼ��������������ʱ��m��ȡֵ��ΧΪ_______��
������6��x��3����ͼ��������������ʱ��m��ȡֵ��ΧΪ_______��
��չ����֪����y��max����x2+2nx����nx����nΪ������n��0������![]() n��3��x��2ʱ������x��������ֵy�ȼ�С������ֱ��д��n��ȡֵ��Χ��
n��3��x��2ʱ������x��������ֵy�ȼ�С������ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҽ�����Ϊ֧Ԯ����������չ���ƻ�Ͷ������ʽ���������ʡ��A��B�������ͼ��ݹ�10��![]() ����A��ͼ���1����B��ͼ���2��������400��Ԫ������A��ͼ���2����B��ͼ���1��������350��Ԫ��
����A��ͼ���1����B��ͼ���2��������400��Ԫ������A��ͼ���2����B��ͼ���1��������350��Ԫ��
��1������A���B��ͼ���ÿ�����������Ԫ��
��2��Ԥ���ڸüƻ���A���B��ͼ�������������ֱ�Ϊ60���˴κ�100���˴�![]() ��������Ͷ��A���B��ͼ��ݵ��ܷ��ò�����1200��Ԫ����ȷ����10��ͼ��ݵ�����������ܺͲ�����680���˴Σ���������쵼���ӽ�ԼͶ�ʷ��ÿ��ǣ�����Ƴ����еķ�����
��������Ͷ��A���B��ͼ��ݵ��ܷ��ò�����1200��Ԫ����ȷ����10��ͼ��ݵ�����������ܺͲ�����680���˴Σ���������쵼���ӽ�ԼͶ�ʷ��ÿ��ǣ�����Ƴ����еķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
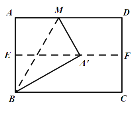
����Ŀ����ͼ�����۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչƽ����һ���۵�ֽƬ��ʹ��A����EF�ϵĵ�A�䴦����ʹ�ۺ۾�����B���õ��ۺ�BM��������ֽƬ�Ŀ�AB=4�����ۺ�BM�ij�Ϊ( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�A��0��0����B��2��0������AP1B�ǵ���ֱ�������Σ��ҡ�P1��90��������AP1B�Ƶ�B˳ʱ����ת180�����õ���BP2C������BP2C�Ƶ�C˳ʱ����ת180�����õ���CP3D���������ƣ��õ��ĵ���ֱ�������ε�ֱ�Ƕ���P2017������Ϊ_____��
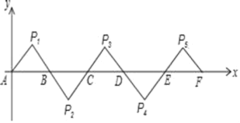
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y = ax2+ bx + c����A��B��C���㣬��֪��A��-3��0����B��0��3����C��1��0����
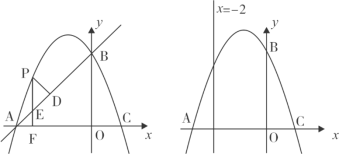
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D������P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
��3����ֱ��x = -2���Ƿ���ڵ�M��ʹ�á�MAC = 2��MCA�������ڣ����M�����꣮�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������͵����ῼ�Ŀ��Խ���Եȼ���ʽ���֣���A��B��C��D�ĸ��ȼ���ijУ���꼶ѧ���μ�����ῼ�������ȡ����ѧ��������ɼ�����ͳ�ƣ����Ƴ�����������������ͳ��ͼ��
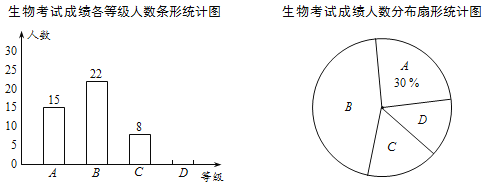
��1����γ������鹲��ȡ�� ��ѧ��������ɼ�������ͳ��ͼ�У�D�ȼ�����Ӧ������Բ�ĽǶ���Ϊ ����
��2��������ͳ��ͼ����������
��3������У���꼶��400��ѧ����������ο����ж�����ѧ��������ɼ��ȼ�ΪD����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com