
【题目】如图,在平面直角坐标系xOy中,抛物线y = ax2+ bx + c经过A、B、C三点,已知点A(-3,0),B(0,3),C(1,0).
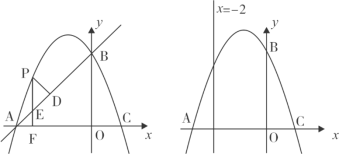
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
(3)在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.
【答案】(1)y=-x2-2x+3;(2)点(-![]() ,
,![]() ),△PDE的周长最大;(3)点M(-2,
),△PDE的周长最大;(3)点M(-2,![]() )或(-2,-
)或(-2,-![]() ).
).
【解析】
(1)将A、B、C三点代入,利用待定系数法求解析式;
(2)根据坐标发现,△AOB是等腰直角三角形,故只需使得PD越大,则△PDE的周长越大.联立直线AB与抛物线的解析式可得交点P坐标;
(3)作点A关于直线x=-2的对称点D,利用∠MAC = 2∠MCA可推导得MD=CD,进而求得ME的长度,从而得出M坐标
解:(1)∵抛物线y=ax2+bx+c经过点A(-3,0),B(0,3),C(1,0),
∴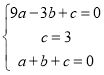 ,解得:
,解得: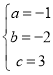 ,
,
所以,抛物线的解析式为y=-x2-2x+3;
(2)∵A(-3,0),B(0,3),
∴OA=OB=3,∴△AOB是等腰直角三角形,∴∠BAO=45°,
∵PF⊥x轴,∴∠AEF=90°-45°=45°,
又∵PD⊥AB,∴△PDE是等腰直角三角形,
∴PD越大,△PDE的周长越大,易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立![]() ,消掉y得,x2+3x+m-3=0,
,消掉y得,x2+3x+m-3=0,
当△=9-4(m-3)=0,即m=![]() 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长,
此时x=-![]() ,y=
,y=![]() ,∴点(-
,∴点(-![]() ,
,![]() ),△PDE的周长最大;
),△PDE的周长最大;
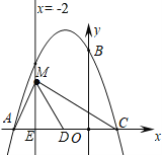
(3)设直线x=-2与x轴交于点E,作点A关于直线x=-2的对称点D,则D(-1,0),连接MA,MD,MC.
∴MA=MD,∠MAC=∠MDA=2∠MCA ,
∴∠CMD=∠DCM
∴MD=CD=2 , ∴ME=![]()
∴点M(-2,![]() )或(-2
)或(-2![]() ).
).


科目:初中数学 来源: 题型:
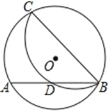
【题目】如图,在⊙O 中,点 C 在优弧 AB 上,将弧 BC 沿直线 BC 折叠后刚好经过弦 AB 的 中点 D.若⊙O 的半径为![]() ,AB=4,则 BC 的长是( )
,AB=4,则 BC 的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲口罩每袋的售价比乙口罩多5元,小明从该药店购买了3袋甲口罩和2袋乙口罩共花费115元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元?
(2)根据消费者需求,药店决定用不超过8000元购进甲、乙两种口罩共400袋.已知甲口罩每袋的进价为22.2元,乙口罩每袋的进价为17.8元,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
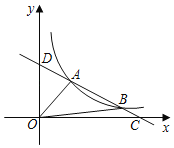
【题目】如图,点A(m,3)、B(6,n)在双曲线y=![]() (x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(1)求双曲线y=![]() 的函数表达式;
的函数表达式;
(2)求△COD的周长;
(3)直接写出不等式![]() -ax>b的解集.
-ax>b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
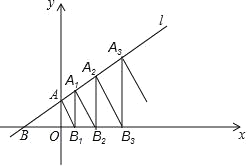
【题目】如图,在平面直角坐标系中,点A,A1,A2,A3…An都在直线1:y=![]() x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
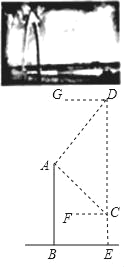
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )

A. ![]() B.
B. ![]() C. 3.5D. 5
C. 3.5D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
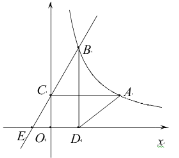
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() .点
.点![]() 为反比例函数图象上的一动点,过点
为反比例函数图象上的一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .直线
.直线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
(1)求反比例函数的表达式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,请求出点
为平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com