
【题目】以△ABC的三边在BC同侧分别作三个等边三角形△ABD,△BCE ,△ACF,试回答下列问题:
(1)四边形ADEF是什么四边形?请证明:
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,四边形ADEF是菱形?
(4)当△ABC满足什么条件时,能否构成正方形?
(5)当△ABC满足什么条件时,无法构成四边形?

【答案】(1)见解析;(2)当△ABC中的∠BAC=150°时,四边形ADEF是矩形;(3)当△ABC中的AB=AC时,四边形ADEF是菱形;(4)当∠BAC=150°且AB=AC时,四边形ADEF是正方形;(5)当∠BAC=60°时,D、A、F为同一直线,与E点构不成四边形,即以A、D、E、F为顶点的四边形不存在.
【解析】
(1)通过证明△DBE≌△ABC,得到DE=AC,利用等边三角形ACF,可得DE=AF,
同理证明![]() 与
与![]() 全等,利用等边三角形
全等,利用等边三角形![]() ,得AD=EF,可得答案.(2)利用平行四边形ADEF是矩形,结合已知条件等边三角形得到
,得AD=EF,可得答案.(2)利用平行四边形ADEF是矩形,结合已知条件等边三角形得到![]() 即可.(3)利用平行四边形ADEF是菱形形,结合已知条件等边三角形得到
即可.(3)利用平行四边形ADEF是菱形形,结合已知条件等边三角形得到![]() 即可.(4)结合(2)(3)问可得答案.(5)当四边形ADEF不存在时,即出现三个顶点在一条直线上,因此可得答案。
即可.(4)结合(2)(3)问可得答案.(5)当四边形ADEF不存在时,即出现三个顶点在一条直线上,因此可得答案。
解:(1) ∵△BCE、△ABD是等边三角形,
∴∠DBA=∠EBC=60°,AB=BD,BE=BC,
∴∠DBE=∠ABC,
∴△DBE≌△ABC,
∴DE=AC,
又△ACF是等边三角形, ∴AC=AF,
∴DE=AF,
同理可证:AD=EF,
∴四边形ADEF是平行四边形.
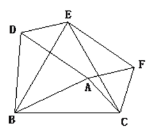
(2) 假设四边形ADEF是矩形, 则∠DAF=90°,
又∠DAB=∠FAC=60°, ∠DAB+∠FAC+∠DAF+∠BAC=360°
∴∠BAC=150°.
因此当△ABC中的∠BAC=150°时,四边形ADEF是矩形.
(3)假设四边形ADEF是菱形, 则AD=DE=EF=AF
∵AB=AD,AC=AF,∴AB=AC
因此当△ABC中的AB=AC时,四边形ADEF是菱形.
(4)结合(2)(3)问可知当∠BAC=150°且AB=AC时,
四边形ADEF是正方形.
(5)由图知道:∠DAB+∠FAC+∠DAF+∠BAC=360°
∴当∠BAC=60°时,D、A、F为同一直线,与E点构不成四边形,
即以A、D、E、F为顶点的四边形不存在.


科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
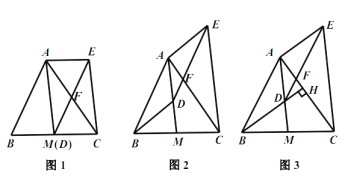
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形
是平行四边形
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中的点A(a,1),t=ab﹣a2﹣b2(a,b是实数)
(1)若关于x的反比例函数y=![]() 过点A,求t的取值范围.
过点A,求t的取值范围.
(2)若关于x的一次函数y=bx过点A,求t的取值范围.
(3)若关于x的二次函数y=x2+bx+b2过点A,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
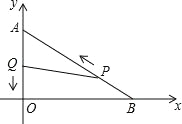
【题目】如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发运动时间为t(s).
(1)t为何值时,△APQ与△AOB相似?
(2)当 t为何值时,△APQ的面积为8cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
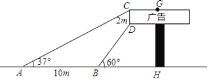
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县古田镇某纪念品商店在销售中发现:“成功从这里开始”的纪念品平均每天可售出20件,每件盈利40元.为了扩大销售量,增加盈利,尽快减少库存,该商店在今年国庆黄金周期间,采取了适当的降价措施,改变营销策略后发现:如果每件降价4元,那么平均每天就可多售出8件.商店要想平均每天在销售这种纪念品上盈利1200元,那么每件纪念品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
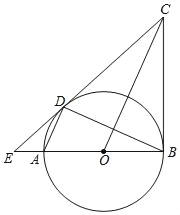
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
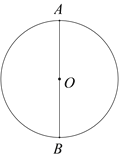
已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
①作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形(_______________)(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD(_______________)(填推理的依据).
∴△ACD是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com