
【题目】下列结论:①几个有理数相乘,若其中负因数有奇数个,则积为负;②两个三次多项式的和一定是三次多项式;③若xyz<0,则![]() +
+![]() +
+![]() +
+![]() 的值为0或﹣4;④若a,b互为相反数,则
的值为0或﹣4;④若a,b互为相反数,则![]() =﹣1;⑤若x=y,则
=﹣1;⑤若x=y,则![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①几个有理数相乘,如果其中一个因数为0,积为0,无论负因数的个数是奇数个还是偶数个;②两个三次多项式的和不一定是三次多项式,也可能三次项合并后为0;③x、y、z可能两个正数一个负数,也可能都是分数,分两种情况求解即可得结论;④根据互为相反数的两个数商为-1但0的相反数为0,即可判断;⑤两个分式的分子和分母都相同,分式的值也相同即可判断.
解:①几个有理数相乘,如果其中一个因数为0,积为0,所以①错误;
②两个三次多项式的和不一定是三次多项式,所以②错误;
③∵xyz<0,
∴分两种情况:一种是两正一负,设x>0,y>0,z<0,
则原式=1+1-1-1=0;
一种是三个数都为负数,
则原式=-1-1-1-1=-4,所以③正确;
④∵0的相反数是0,![]() 无意义,∴若a,b互为相反数,则
无意义,∴若a,b互为相反数,则![]() =﹣1不正确,所以④错误;
=﹣1不正确,所以④错误;
⑤两个分式的分子和分母都相等,则两个分式相等,所以⑤正确.
故选:B.


科目:初中数学 来源: 题型:
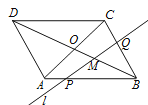
【题目】如右上图,直线l截□ABCD的边AB、BC和对角线BD于P、Q、M,对角线AC、BD
相交于点O,且PB=3PA,CQ︰BQ=1︰2,则BM︰BO=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)求降价前农民手中的钱数y与售出的土豆千克数x的函数关系式;
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
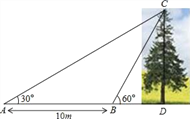
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】8.7米
【解析】试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×![]() =5
=5![]() ≈5×1.732=8.7(米).
≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
考点:解直角三角形的应用
【题型】解答题
【结束】
23
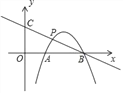
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
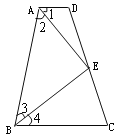
【题目】如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
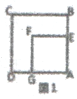
【题目】发现来源于探究。小亮进行数学探究活动,作边长为a的正方形ABCD和边长边b的正方形AEFG(a>b),开始时点E在AB上,如图1,将正方形AEFG绕点A逆时针方向旋转。
(1)如图2,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,请证明:△ADG≌△ABE;
(2)如图3,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,当点G恰好落在线段BE上,且a=3,b=2时,请你帮他求此时DG的长。
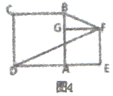
(3)如图4,小亮旋转正方形AEFG,当点E在DA的延长线上时,连接BF、DF,若FG平分∠BFD,请你帮他求a:b的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度同时沿直线AB向左运动(C在线段AP上,D在线段BP上),运动时间为ts
(I)若C、D运动1s时,且PD=2AC,求AP的长;
(II)若C、D运动到任一时刻时,总有PD=2AC,AP的长度是否变化?若不变,请求出AP的长;若变化,请说明理由;
(III)在(II)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
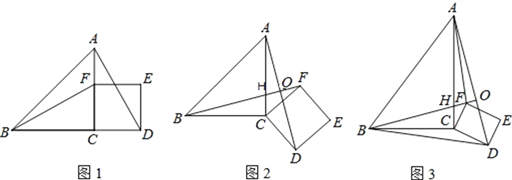
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形。图2中BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=![]() ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com