
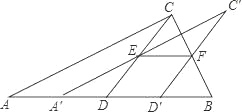
【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
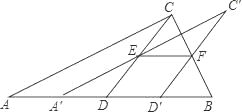
【答案】△A′DE是等腰三角形;证明过程见解析.
【解析】试题分析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.
试题解析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB,
∴CD=DA=DB,
∴∠DAC=∠DCA,
∵A′C∥AC,
∴∠DA′E=∠A,∠DEA′=∠DCA,
∴∠DA′E=∠DEA′,
∴DA′=DE,
∴△A′DE是等腰三角形.
∵四边形DEFD′是菱形,
∴EF=DE=DA′,EF∥DD′,
∴∠CEF=∠DA′E,∠EFC=∠CD′A′,
∵CD∥C′D′,
∴∠A′DE=∠A′D′C=∠EFC,
在△A′DE和△EFC′中,
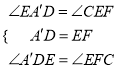 ,
,
∴△A′DE≌△EFC′.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】用配方法解方程x2-8x+7=0,则配方正确的是( )
A. (x+4)2=9 B. (x﹣4)2=9 C. (x﹣8)2=16 D. (x+8)2=57
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:
①x<0时,![]() ;②△OPQ的面积为定值; ③x>0时,y随x的增大而增大; ④MQ=2PM;⑤∠POQ可以等于90°.
;②△OPQ的面积为定值; ③x>0时,y随x的增大而增大; ④MQ=2PM;⑤∠POQ可以等于90°.
其中正确结论是( )
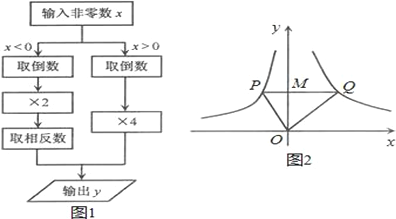
A. ①②④ B. ②④⑤ C. ③④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元,则符合该公司要求的购买方式有( )
A. 3种 B. 4种 C. 5种 D. 6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂专门安排160名工人手工缝制衬衣,每件衬衣由2个衣袖、1个衣身组成,如果每人每天能够缝制衣袖10个或衣身15个,那么应安排________名工人缝制衣袖,才能使每天缝制出的衣袖、衣身正好配套。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈做了一份美味可口的菜品,为了了解菜品的咸淡是否适合,于是妈妈取了一点品尝,属于_________________ (填“普查”或“ 抽样调查”)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
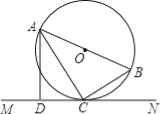
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com