
【题目】已知二次函数y=(t+1)x2+2(t+2)x+![]() 在x=0和x=2时的函数值相等.
在x=0和x=2时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(-3,m),求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,求n的取值范围.
【答案】(1)![]() (2)① m=-6,k=4;②
(2)① m=-6,k=4;②![]()
【解析】
(1)把x=0和x=2代入得出关于t的方程,求出t即可;
(2)把A的坐标代入抛物线,即可求出m,把A的坐标代入直线,即可求出k;
(3)求出点B、C间的部分图象的解析式是y=-![]() (x-3)(x+1),得出抛物线平移后得出的图象G的解析式是y=-
(x-3)(x+1),得出抛物线平移后得出的图象G的解析式是y=-![]() (x-3+n)(x+1+n),-n-1≤x≤3-n,直线平移后的解析式是y=4x+6+n,若两图象有一个交点时,得出方程4x+6+n=-
(x-3+n)(x+1+n),-n-1≤x≤3-n,直线平移后的解析式是y=4x+6+n,若两图象有一个交点时,得出方程4x+6+n=-![]() (x-3+n)(x+1+n)有两个相等的实数解,求出判别式△=6n=0,求出的n的值与已知n>0相矛盾,得出平移后的直线与抛物线有两个公共点,设两个临界的交点为(-n-1,0),(3-n,0),代入直线的解析式,求出n的值,即可得出答案.
(x-3+n)(x+1+n)有两个相等的实数解,求出判别式△=6n=0,求出的n的值与已知n>0相矛盾,得出平移后的直线与抛物线有两个公共点,设两个临界的交点为(-n-1,0),(3-n,0),代入直线的解析式,求出n的值,即可得出答案.
(1)解:∵二次函数y=(t+1)x2+2(t+2)x+![]() 在x=0和x=2时的函数值相等,
在x=0和x=2时的函数值相等,
∴代入得:0+0+![]() =4(t+1)+4(t+2)+
=4(t+1)+4(t+2)+![]() ,
,
解得:t=-![]() ,
,
∴y=(-![]() +1)x2+2(-
+1)x2+2(-![]() +2)x+
+2)x+![]() =-
=-![]() x2+x+
x2+x+![]() ,
,
∴二次函数的解析式是y=-![]() x2+x+
x2+x+![]() .
.
(2)解:把A(-3,m)代入y=-![]() x2+x+
x2+x+![]() 得:m=-
得:m=-![]() ×(-3)2-3+
×(-3)2-3+![]() =-6,
=-6,
即A(-3,-6),
代入y=kx+6得:-6=-3k+6,
解得:k=4,
即m=-6,k=4.
(3)解:由题意可知,点B、C间的部分图象的解析式是y=-![]() x2+x+
x2+x+![]() =-
=-![]() (x2-2x-3)=-
(x2-2x-3)=-![]() (x-3)(x+1),-1≤x≤3,
(x-3)(x+1),-1≤x≤3,
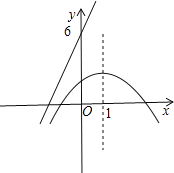
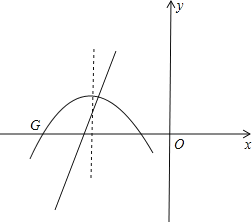
则抛物线平移后得出的图象G的解析式是y=-![]() (x-3+n)(x+1+n),-n-1≤x≤3-n,
(x-3+n)(x+1+n),-n-1≤x≤3-n,
此时直线平移后的解析式是y=4x+6+n,
如果平移后的直线与平移后的二次函数相切,
则方程4x+6+n=-![]() (x-3+n)(x+1+n)有两个相等的实数解,
(x-3+n)(x+1+n)有两个相等的实数解,
即-![]() x2-(n+3)x-
x2-(n+3)x-![]() n2-
n2-![]() =0有两个相等的实数解,
=0有两个相等的实数解,
判别式△=[-(n+3)]2-4×(-![]() )×(-
)×(-![]() n2-
n2-![]() )=6n=0,
)=6n=0,
即n=0,
∵与已知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(-n-1,0),(3-n,0),
则0=4(-n-1)+6+n,
n=![]() ,
,
0=4(3-n)+6+n,
n=6,
即n的取值范围是:![]() ≤n≤6.
≤n≤6.


科目:初中数学 来源: 题型:
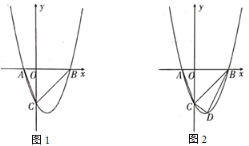
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
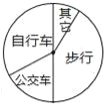
【题目】某学校要了解学生上学交通情况,选取七年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知七年级乘公交车上学的人数为50人.
(1)七年级学生中,骑自行车和乘公交车上学的学生人数哪个更多?多多少人?
(2)如果全校有学生2400人,学校准备的600个自行车停车位是否足够?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=4,BC=2,点O在AB的延长线上,OB=![]() ,∠AOE=60°,动点P从点O出发,以每秒2个单位长度的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从B点出发,以每秒1个单位长度的速度沿折线B-C-D向点D运动,Q与D重合时,P,Q同时停止运动,设P的运动时间t秒.
,∠AOE=60°,动点P从点O出发,以每秒2个单位长度的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从B点出发,以每秒1个单位长度的速度沿折线B-C-D向点D运动,Q与D重合时,P,Q同时停止运动,设P的运动时间t秒.
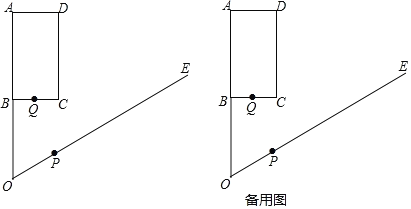
(1)∠BOC= ,PA的最小值是 ;
(2)当⊙P过点C时,求⊙P的劣弧与线段OA围成的封闭图形的面积;
(3)当⊙P与矩形ABCD的边所在直线相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°.
求作:射线CG,使得CG∥AB.
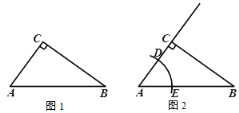
下面是小东设计的尺规作图过程.
作法:
①以点A为圆心,适当长为半径作弧,分别交AC,AB于D,E两点;
②以点C为圆心,AD长为半径作弧,交AC的延长线于点F;
③以点F为圆心,DE长为半径作弧,两弧在∠FCB内部交于点G;
④作射线CG.所以射线CG就是所求作的射线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接FG、DE.
∵△ADE ≌ △_________,
∴∠DAE = ∠_________.
∴CG∥AB(___________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,我校将在周末举行“亲近大自然”的社会实践活动,现随机抽取了部分学生进行主题为“你最想去的景点是千鹤湖公园”的问卷调查,要求学生只能从“A(华中工委纪念馆),B(洋马菊花园),C(千鹤湖公园),D(丹顶鹤自然保护区)”四个景点中选择一项,根据调查结果,绘制了如图的两幅不完整的统计图:
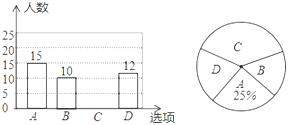
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求B所占的圆心角度数;
(4)若该校有3600名学生,试估计该校最想去千鹤湖公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx,过点A(4,0)和点B(6,2![]() ),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
(1)求抛物线的解析式,并直接写出点D的坐标;
(2)当△AMN的周长最小时,求t的值;
(3)如图②,过点M作ME⊥x轴,交抛物线y=ax2+bx于点E,连接EM,AE,当△AME与△DOC相似时.请直接写出所有符合条件的点M坐标.
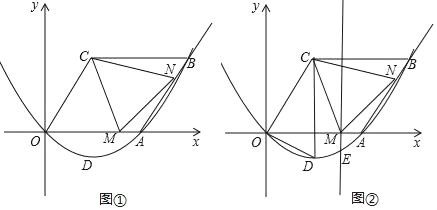
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求a的值;
(2)若PN:MN=1:3,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() BP2的最小值.
BP2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com