
【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
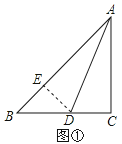

(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;
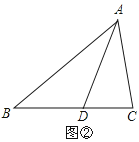
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
【答案】(1)(2)见解析
【解析】(1)首先在AB上截取AE=AC,连接DE,易证△ADE≌△ADC(SAS),则可得∠AED=∠C,ED=CD,又由∠ACB=2∠B,易证DE=CD,则可求得AB=AC+CD;
(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD≌△CAD,可得ED=CD,∠AED=∠ACD,又由∠ACB=2∠B,易证DE=EB,则可求得AC+AB=CD.
解:(1)猜想:AB=AC+CD.
证明:如图,在AB上截取AE=AC,连接DE,
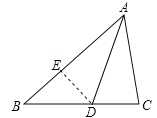
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
∵AD=AD,
∴△ADE≌△ADC(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:如图,在BA的延长线上截取AE=AC,连接ED.

∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD.
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB.
又∠ACB=2∠B,∠FED=∠B+∠EDB,∠EDB=∠B.
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.
“点睛”此题考查了全等三角形的判定与性质以及等腰三角形的判定定理.此题难度适中,解题的关键是注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有一列数,按一定规律排列成1,-4,16,-64,256…
(1)第11个数是 (写成幂的形式)
(2)若其中三个相邻的数的和为3328,求这三个数各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|= 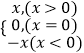 ,
,
所以当x>0时, ![]() =
= ![]() =1; 当x<0时,
=1; 当x<0时, ![]() =
= ![]() =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, ![]() +
+ ![]() =;
=;
(2)已知a,b是有理数,当abc≠0时, ![]() +
+ ![]() +
+ ![]() =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.

(1)画出△A1B1C1,使它与△ABC关于直线a对称;
(2)求出△A1B1C1的面积.
(3)在直线a上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com