
分析 (1)将x=1000代入y求得y值即可求得销售价格,代入w内=x(y-20)-62500即可求得月利润;
(2)先运用二次函数的性质求出w内取最大值时x的值,再根据w外的最大值等于w内的最大值,列出关于a的方程,解方程即可求出a的值;
(3)先分别求出当x=5000时,w内与w外的值,再分w内<w外,w内=w外,w内>w外这三种情况进行讨论,即可求出a的取值范围.
解答 解:(1)∵销售价格y(元/件)与月销量x(件)的函数关系式为y=-$\frac{1}{100}$x+150,
∴当x=1000时,y=-10+150=140,w内=x(y-20)-62500=1000×120-62500=57500,
∴当销量为1000件时,销售价格为140元,月利润为57500元;
w内=x(y-20)-62500=x(-$\frac{1}{100}$x+150-20)-62500=-$\frac{1}{100}$x2+130x-62500,
即w内=-$\frac{1}{100}$x2+130x-62500=-$\frac{1}{100}$(x-6500)2+360000,
∴当销量为6500件时有最大利润360000元;
(2)w外=x(150-a)-$\frac{1}{100}$x2=-$\frac{1}{100}$x2+(150-a)x,
即w外=-$\frac{1}{100}$x2+(150-a)x;
∵在国外销售月利润的最大值与在国内销售月利润的最大值相同,
$\frac{0-(150-a)^{2}}{4×(-\frac{1}{100})}$=360000
解得a1=30,a2=270(不合题意,舍去).
所以 a=30;
(3)当x=5000时,w内=-$\frac{1}{100}$×50002+130×5000-62500=337500,
w外=-$\frac{1}{100}$×50002+(150-a)×5000=-5000a+500000.
若w内<w外,即当a<32.5时,在国外销售才能使所获月利润较大;
若w内=w外,即当a=32.5时,在国内、外销售所获月利润一样大;
w内>w外,即当a>32.5时,在国内销售才能使所获月利润较大
点评 本题考查了二次函数在实际生活中的应用,难度适中,根据利润的关系式分别写出w内,w外与x间的函数关系式是解题的关键.


科目:初中数学 来源: 题型:选择题
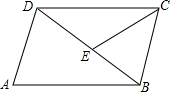 如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )
如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y3<y2 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y2<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
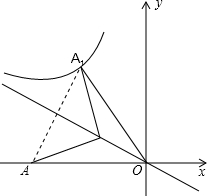 如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )
如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )| A. | -12 | B. | -12$\sqrt{5}$ | C. | -24 | D. | -48 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com