
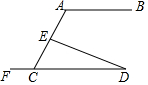
 如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )
如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
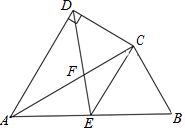 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,E为AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )
两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )| A. | 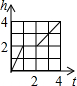 | B. |  | C. | 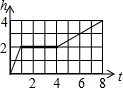 | D. | 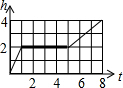 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:
如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com