
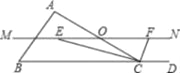
【题目】如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.
(1)求证:EO=FO;(2)若CE=4,CF=3,你还能得到那些结论?
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )

①DF平分∠BDE;②△BFD是等腰三角形;;③△CED的周长等于BC的长.
A. 0个; B. 1个; C. 2个; D. 3个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
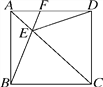
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 和
和![]() ,且
,且![]() .
.
![]()
(1)求线段![]() 的长;
的长;
(2)点![]() 在数轴上所对应的数为
在数轴上所对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,点
的解,点![]() 在线段
在线段![]() 上,并且
上,并且![]()
![]() ,请求出点
,请求出点![]() 在数轴上所对应的数;
在数轴上所对应的数;
(3)在(2)的条件下,线段![]() 和
和![]() 分别以
分别以![]() 个单位长度/秒和
个单位长度/秒和![]() 个单位长度/秒的速度同时向右运动,运动时间为
个单位长度/秒的速度同时向右运动,运动时间为![]() 秒,
秒,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E. 
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com