
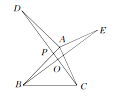
【题目】如图所示,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,AB和CD相交于P,则∠DOE的度数是____.
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
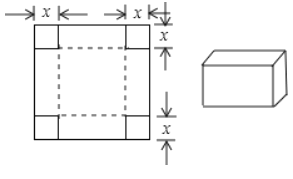
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.
(1)直尺的长为多少个单位长度(直接写答案)
(2)如图2,直尺AB在数轴上移动,有BC=4OA,求此时A点对应的数;
(3)如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2, 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)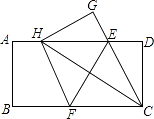
查看答案和解析>>
科目:初中数学 来源: 题型:
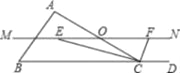
【题目】如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.
(1)求证:EO=FO;(2)若CE=4,CF=3,你还能得到那些结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
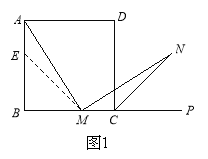
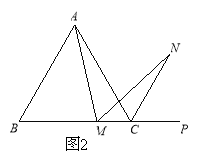
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. 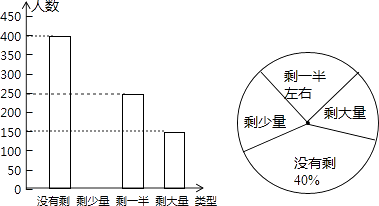
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县“果菜大王”王大炮收货番茄20吨,青椒12吨.现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售,已知一辆甲种货车可装番茄4吨和青椒1吨,一辆乙种货车可装番茄和青椒各2吨.
(1)王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王大炮应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com