
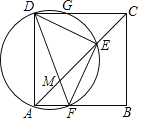
【题目】如图,已知在正方形ABCD中,连结AC,在AC上截取AE=AD,作△ADE的外接圆交AB于点F,连结DF交AC于点M,连结EF,下列选项不正确的是( )
A.![]()
B.AM=EC
C.∠EFB=∠AFD
D.S四边形BCMF=S四边形ADEF
【答案】D
【解析】
连接FG,根据正方形的性质得到∠DAF=∠ADC=90°,由圆周角定理得到∠DGF=90°,推出四边形AFGD是矩形,得到DG=AF,求得![]() =
=![]() ,故A正确;根据等腰三角形的性质得到∠ADE=∠AED,等量代换得到∠EFB=∠AFD,故C正确;推出△DEF是等腰直角三角形,得到DE=EF,根据全等三角形的性质得到∠AEF=∠ADF=∠CDE,再证明△ADM≌△CDE即可得到,故B正确;连接BE,求得S四边形ADEF=S△ADE+S△AEF=S△ADE+S△CDE=S△ACD=S△ABC,由于S四边形BCMF<S△ABC,得到S四边形BCMF<S四边形ADEF,故D错误.
,故A正确;根据等腰三角形的性质得到∠ADE=∠AED,等量代换得到∠EFB=∠AFD,故C正确;推出△DEF是等腰直角三角形,得到DE=EF,根据全等三角形的性质得到∠AEF=∠ADF=∠CDE,再证明△ADM≌△CDE即可得到,故B正确;连接BE,求得S四边形ADEF=S△ADE+S△AEF=S△ADE+S△CDE=S△ACD=S△ABC,由于S四边形BCMF<S△ABC,得到S四边形BCMF<S四边形ADEF,故D错误.
解:连接FG,
∵四边形ABCD是正方形,
∴∠DAF=∠ADC=90°,
∴DF是圆的直径,
∴∠DGF=90°,
∴四边形AFGD是矩形,
∴DG=AF,
∴![]() =
=![]() ,故A正确;
,故A正确;
∵AD=AE,
∴∠ADE=∠AED,
∵∠AFD=∠AED,∠BFE=∠ADE,
∴∠EFB=∠AFD,故C正确;
∵DF是圆的直径,
∴∠DEF=90°,
∵∠DFE=∠DAC=45°,
∴△DEF是等腰直角三角形,
∴DE=EF,
∵∠CDE+∠ADE=∠AEF+∠AED=90°,
∴∠CDE=∠EAF,
∴△CDE≌△AEF(SAS),
∴∠AEF=∠ADF=∠CDE,
又∵AD=CD,∠DAM=∠ECD=45°,
∴△ADM≌△CDE,
∴AM=CE,故B正确;
连接BE,
∵AE=BC=AD,CE=AF,∠CAF=∠BCE=45°,
∴△AEF≌△CBE(SAS),
∴S四边形ADEF=S△ADE+S△AEF=S△ADE+S△CDE=S△ACD=S△ABC,
∵S四边形BCMF<S△ABC,
∴S四边形BCMF<S四边形ADEF,故D错误,
故选:D.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
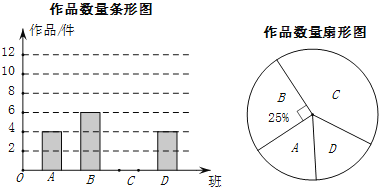
【题目】某中学参加“创文明城市”书画比赛时,老师从全校![]() 个班中随机抽取了
个班中随机抽取了![]() 个班(用
个班(用![]() 表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题:
表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题:
(1)老师采用的调查方式是 .(填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中![]() 班作品数量所对应的圆心角度数 度.
班作品数量所对应的圆心角度数 度.
(3)请估计全校共征集作品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
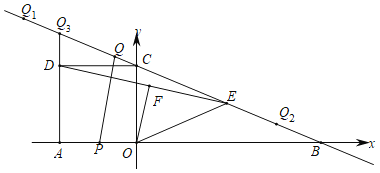
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
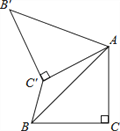
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某配餐公司有A,B两种营养快餐。一天,公司售出两种快餐共640份,获利2160元。两种快餐的成本价、销售价如下表。
A种快餐 | B种快餐 | |
成本价 | 5元/份 | 6元/份 |
销售价 | 8元/份 | 10元/份 |
(1)求该公司这一天销售A、B两种快餐各多少份?
(2)为扩大销售,公司决定第二天对一定数量的A、B两种快餐同时举行降价促销活动。降价的A、B两种快餐的数量均为第一天销售A、B两种快餐数量的2倍,且A种快餐按原销售价的九五折出售,若公司要求这些快餐当天全部售出后,所获的利润不少于3280元,那么B种快餐最低可以按原销售价打几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
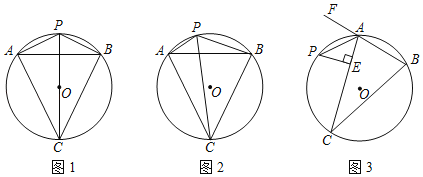
【题目】(1)已知等边△ABC内接于⊙O.点P为![]() 上的一个动点,连结PA、PB、PC.
上的一个动点,连结PA、PB、PC.
①如图1,当线段PC经过点O时,试写出线段PA,PB,PC之间满足的等量关系,并说明理由;
②如图2,点P为![]() 上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论;
上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论;
(2)如图3,在△ABC中,AB=4,AC=7,∠BAC的外角平分线交△ABC的外接圆于点P,PE⊥AC于E,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
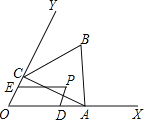
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校3男2女共5名学生参加黄石市教育局举办的“我爱黄石”演讲比赛.
(1)若从5名学生中任意抽取3名,共有多少种不同的抽法,列出所有可能情形;
(2)若抽取的3名学生中,某男生抽中,且必有1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
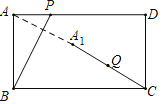
【题目】如图在矩形ABCD中,AB=![]() ,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1,连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1,连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.![]() πB.
πB.![]() πC.
πC.![]() πD.π
πD.π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com