
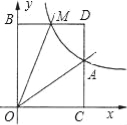
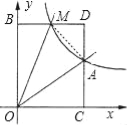
【题目】如图,已知反比例函数y=![]() 的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
(1)求反比例函数的解析式;
(2)当∠OAM=90°时,求点M的坐标.
【答案】(1)、y=![]() ;(2)、(
;(2)、(![]() ,4).
,4).
【解析】
试题分析:(1)、把A点坐标代入y=![]() 中求出k的值即可;(2)、先证明Rt△AMD∽Rt△OAC得到(n﹣1):2=(2﹣m):1,再利用点M(m,n)在y=
中求出k的值即可;(2)、先证明Rt△AMD∽Rt△OAC得到(n﹣1):2=(2﹣m):1,再利用点M(m,n)在y=![]() 的图象上得到n=
的图象上得到n=![]() ,然后解关于m的方程求出m,从而可得到M点的坐标.
,然后解关于m的方程求出m,从而可得到M点的坐标.
试题解析:(1)、把A(2,1)代入y=![]() 得k=2×1=2, 所以反比例函数解析式为y=
得k=2×1=2, 所以反比例函数解析式为y=![]() ;
;
(2)、∵∠OAM=90°, ∴∠MAD+∠CAO=90°, 而∠CAO+∠AOC=90°, ∴∠AOC=∠MAD,
∴Rt△AMD∽Rt△OAC, ∴AD:OC=MD:AC,即(n﹣1):2=(2﹣m):1,
∴n﹣1=4﹣2m, ∵点M(m,n)在y=![]() 的图象上, ∴n=
的图象上, ∴n=![]() , ∴
, ∴![]() ﹣1=4﹣2m,
﹣1=4﹣2m,
整理得2m2﹣5m+2=0,解得m1=![]() ,m2=2(舍去), ∴n=4, ∴点M的坐标为(
,m2=2(舍去), ∴n=4, ∴点M的坐标为(![]() ,4).
,4).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适合普查的事件是( )
A.调查华为手机的使用寿命
B.调查市九年级学生的心理健康情况
C.调查你班学生打网络游戏的情况
D.调查中央电视台《中国舆论场》的节目收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,0),(5,0),图象上有三个点(x1,y1),(x2,y2),(x3,y3).若当x1<﹣1<x2<5<x3时,均有y1y2<0,y2y3<0,则下列说法中正确的是( )
A.a<0 B.x=2时,y有最大值
C.y1y2y3<0 D.5b=4c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金.该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元).若想让一半左右的营业员都能达到月销售目标,则月销售额定为_____万元较为合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过平移后,使点A与点A′(﹣1,4)重合.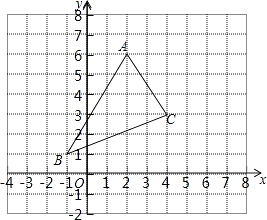
(1)画出平移后的△A′B′C′;
(2)求出△A′B′C′的面积;
(3)若三角形ABC内有一点P(a,b),经过平移后的对应点P′的坐标;
(4)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com