
【题目】已知,如图1,![]() 为正方形
为正方形![]() 边
边![]() 的中点,
的中点,![]() ,连接
,连接![]() ,
,![]() .
.
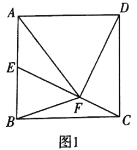
(1)求证:①![]() ;
;
②![]() ;
;
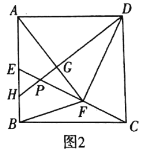
(2)如图2,若![]() ,作
,作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)①见详解,②见详解;(2)2
【解析】
(1)①由![]() 为正方形
为正方形![]() 边
边![]() 的中点,得BE=
的中点,得BE=![]() ,易证DFC~CBE,得
,易证DFC~CBE,得![]() ,进而即可得到结论;②过点F作FM⊥AD,垂足为点M,CF=a,则DF=2a,DC=
,进而即可得到结论;②过点F作FM⊥AD,垂足为点M,CF=a,则DF=2a,DC=![]() ,用含a得代数式表示出AF的长,进而得到AF= AB,即可得到结论;
,用含a得代数式表示出AF的长,进而得到AF= AB,即可得到结论;
(2)过点F作FM⊥AD,垂足为点M,由第(1)②小题,可知:a=![]() ,得到DG=MF=
,得到DG=MF=![]() ,由余弦函数的定义得
,由余弦函数的定义得![]() ,从而得到DH,AH,EH的长,结合
,从而得到DH,AH,EH的长,结合![]() ,即可求解.
,即可求解.
(1)①∵![]() 为正方形
为正方形![]() 边
边![]() 的中点,
的中点,
∴BE=![]() ,
,
∵在正方形ABCD中,![]() ,
,
∴∠CDF+∠DCF=90°,∠DCF+∠ECB=90°,
∴∠CDF=∠ECB,
又∵∠DFC=∠CBE=90°,
∴DFC~CBE,
∴![]() =
=![]() ,即:
,即:![]() ;
;
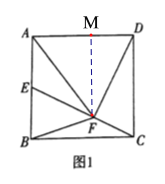
②过点F作FM⊥AD,垂足为点M,
∴FM∥CD,
∴∠MFD=∠CDF,
∴在Rt MFD与Rt CDF中,tan∠MFD=tan∠CDF=![]() =
=![]() ,
,
设CF=a,则DF=2a,DC=![]() ,
,
∵tan∠MFD=![]() =
=![]() ,DF2=MD2+MF2,
,DF2=MD2+MF2,
∴MD:MF:DF=1:2:![]() ,
,
∴MD=![]() =
=![]() ,MF=2MD=
,MF=2MD=![]() ,
,
∵AD= DC=![]() ,
,
∴AM= AD- MD=![]() ,
,
∴AF=![]() =
=![]() ,
,
∵AB=CD=![]() ,
,
∴AF= AB,
∴![]() ;
;
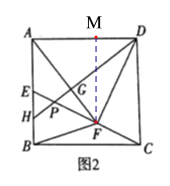
(2)过点F作FM⊥AD,垂足为点M,
由(1)②小题可知:![]() ,即:a=
,即:a=![]() ,
,
∴MF=![]() =
=![]() ,AD=AB=CD=8,
,AD=AB=CD=8,
∵AB=AF=AD,![]() ,FM⊥AD,
,FM⊥AD,![]()
∴DG=MF=![]() ,
,
∵cos∠ADH=![]() ,
,
∴DH=![]() =
=![]() =10,
=10,
∴AH=![]() ,
,
∵AE=![]() AB=4,
AB=4,
∴EH=6-4=2,
∵AB∥CD,
∴![]() ,即:
,即:![]() ,
,
∴HP=2.


科目:初中数学 来源: 题型:
【题目】2019年10月17日是我国第6个扶贫日,也是第27个国际消除贫困日.为组织开展好铜陵市2019年扶贫日系列活动,促进我市贫困地区农产品销售,增加贫困群众收入,加快脱贫攻坚步伐.我市决定将一批铜陵生姜送往外地销售.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱生姜,且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少箱生姜?
(2)如果这批生姜有1520箱,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了40箱,其它装满,求甲、乙两种货车各有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
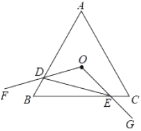
【题目】如图,等边![]() 边长为
边长为![]() ,点
,点![]() 是
是![]() 的内心,
的内心,![]() ,绕点
,绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 形状不变;②
形状不变;②![]() 的面积最小不会小于四边形
的面积最小不会小于四边形![]() 的面积的四分之一;③四边形
的面积的四分之一;③四边形![]() 的面积始终不变;④
的面积始终不变;④![]() 周长的最小值为
周长的最小值为![]() .上述结论中正确的个数是( )
.上述结论中正确的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
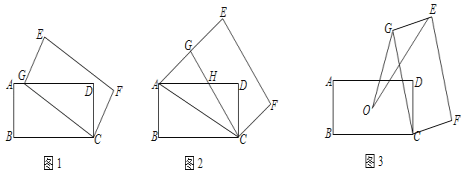
【题目】矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).
(1)如图1,当点G落在AD边上时,直接写出AG的长为 ;
(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;
(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
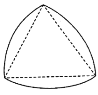
【题目】勒洛三角形是以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形,如图所示,若等边三角形的边长为1,则该勒洛三角形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
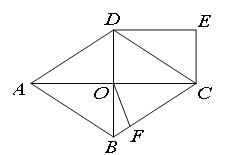
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上.若BC=1,GH=2,则CG的长为( )
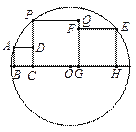
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com