
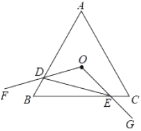
【题目】如图,等边![]() 边长为
边长为![]() ,点
,点![]() 是
是![]() 的内心,
的内心,![]() ,绕点
,绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 形状不变;②
形状不变;②![]() 的面积最小不会小于四边形
的面积最小不会小于四边形![]() 的面积的四分之一;③四边形
的面积的四分之一;③四边形![]() 的面积始终不变;④
的面积始终不变;④![]() 周长的最小值为
周长的最小值为![]() .上述结论中正确的个数是( )
.上述结论中正确的个数是( )
A.4B.3C.2D.1
【答案】A
【解析】
连接OB、OC,利用SAS证出△ODB≌△OEC,从而得出△ODE是顶角为120°的等腰三角形,即可判断①;过点O作OH⊥DE,则DH=EH,利用锐角三角函数可得OH=![]() OE和DE=
OE和DE=![]() OE,然后三角形的面积公式可得S△ODE=
OE,然后三角形的面积公式可得S△ODE=![]() OE2,从而得出OE最小时,S△ODE最小,根据垂线段最短即可求出S△ODE的最小值,然后证出S四边形ODBE=S△OBC=
OE2,从而得出OE最小时,S△ODE最小,根据垂线段最短即可求出S△ODE的最小值,然后证出S四边形ODBE=S△OBC=![]() 即可判断②和③;求出
即可判断②和③;求出![]() 的周长=a+DE,求出DE的最小值即可判断④.
的周长=a+DE,求出DE的最小值即可判断④.
解:连接OB、OC
∵![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的内心,
的内心,
∴∠ABC=∠ACB=60°,BO=CO,BO、CO平分∠ABC和∠ACB
∴∠OBA=∠OBC=![]() ∠ABC=30°,∠OCA=∠OCB=
∠ABC=30°,∠OCA=∠OCB=![]() ∠ACB=30°
∠ACB=30°
∴∠OBA=∠OCB,∠BOC=180°-∠OBC-∠OCB=120°
∵![]()
∴![]() ∠BOC
∠BOC
∴∠FOG-∠BOE=∠BOC-∠BOE
∴∠BOD=∠COE
在△ODB和△OEC中
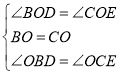
∴△ODB≌△OEC
∴OD=OE
∴△ODE是顶角为120°的等腰三角形,
∴![]() 形状不变,故①正确;
形状不变,故①正确;
过点O作OH⊥DE,则DH=EH
∵△ODE是顶角为120°的等腰三角形
∴∠ODE=∠OED=![]() (180°-120°)=30°
(180°-120°)=30°
∴OH=OE·sin∠OED=![]() OE,EH= OE·cos∠OED=
OE,EH= OE·cos∠OED=![]() OE
OE
∴DE=2EH=![]() OE
OE
∴S△ODE=![]() DE·OH=
DE·OH=![]() OE2
OE2
∴OE最小时,S△ODE最小,
过点O作OE′⊥BC于E′,根据垂线段最短,OE′即为OE的最小值

∴BE′=![]() BC=
BC=![]()
在Rt△OBE′中
OE′=BE′·tan∠OBE′=![]() ×
×![]() =
=![]()
∴S△ODE的最小值为![]() OE′2=
OE′2=![]()
∵△ODB≌△OEC
∴S四边形ODBE=S△ODB+S△OBE= S△OEC+S△OBE=S△OBC=![]() BC·OE′=
BC·OE′=![]()
∵![]() =
=![]() ×
×![]()
∴S△ODE≤![]() S四边形ODBE
S四边形ODBE
即![]() 的面积最小不会小于四边形
的面积最小不会小于四边形![]() 的面积的四分之一,故②正确;
的面积的四分之一,故②正确;
∵S四边形ODBE=![]()
∴四边形![]() 的面积始终不变,故③正确;
的面积始终不变,故③正确;
∵△ODB≌△OEC
∴DB=EC
∴![]() 的周长=DB+BE+DE= EC+BE+DE=BC+DE=a+DE
的周长=DB+BE+DE= EC+BE+DE=BC+DE=a+DE
∴DE最小时![]() 的周长最小
的周长最小
∵DE=![]() OE
OE
∴OE最小时,DE最小
而OE的最小值为OE′=![]()
∴DE的最小值为![]() ×
×![]() =
=![]()
∴![]() 的周长的最小值为a+
的周长的最小值为a+![]() =
=![]() ,故④正确;
,故④正确;
综上:4个结论都正确,
故选A.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一动点(不与点B、C重合),延长AE到点F,连接BF,且∠AFB=45°,G为DC边上一点,且DG=BE,连接DF,点F关于直线AB的对称点为M,连接AM、BM.
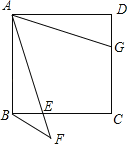
(1)依据题意,补全图形;
(2)求证:∠DAG=∠MAB;
(3)用等式表示线段BM、DF与AD的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全体同学参加了“关怀贫困学生”爱心捐款活动,该校随机抽查了七、八、九三个年级部分学生捐款情况,将结果绘制成两幅不完整的统计图.根据图中的信息,解决下列问题:
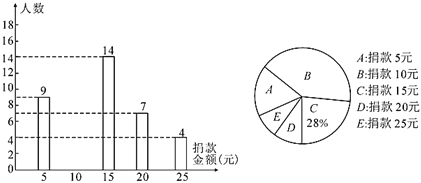
(1)这次共抽查了_______名学生进行统计,其中![]() 类所对应扇形的圆心角的度数为________;
类所对应扇形的圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校有![]() 名学生,估计该校捐款
名学生,估计该校捐款![]() 元的学生有多少人?
元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和2.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,将
上,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,又将
处,又将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在直线
落在直线![]() 与
与![]() 的交点
的交点![]() 处.
处.
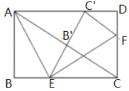
(1)求证:点![]() 在
在![]() 的角平分线上;
的角平分线上;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
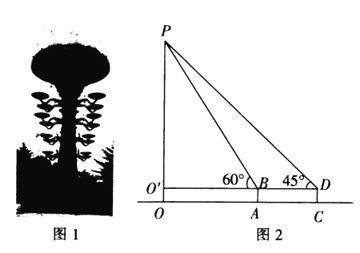
【题目】如图1所示的是宝鸡市文化景观标志“天下第一灯”,它由国际![]() 不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分
不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分![]() 层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部
层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部![]() 他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点
他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点![]() 并在点
并在点![]() 处安装了测量器
处安装了测量器![]() 在点
在点![]() 处测得该灯的顶点P的仰角为
处测得该灯的顶点P的仰角为![]() ;再在
;再在![]() 的延长线上确定一点
的延长线上确定一点![]() 使
使![]() 米,在
米,在![]() 点处测得该灯的顶点
点处测得该灯的顶点![]() 的仰角为
的仰角为![]() .若测量过程中测量器的高度始终为
.若测量过程中测量器的高度始终为![]() 米,求“天下第一灯”的高度.
米,求“天下第一灯”的高度.![]() ,最后结果取整数)
,最后结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,⊙O分别切AB于M,BC于N,连接BO、CO,BO=CO.

(1)求证:AC是⊙O的切线;
(2)连接MC,若![]() ,求sin∠B的值.
,求sin∠B的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com