
| A�� | $\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=5.5}\\{y=-1}\end{array}\right.$ |
���� ��������õ�����x��y�Ķ�Ԫһ�η�����$\left\{\begin{array}{l}{x+1=6��}\\{x-2y=7��}\end{array}\right.$���ⷽ���鼴����⣮
��� �⣺��������$\left\{\begin{array}{l}{x+1=6��}\\{x-2y=7��}\end{array}\right.$��
��ٵ�x=5��
��x=5����ڵ�5-2y=7�����y=-1��
�ʷ����� $\left\{\begin{array}{l}{5��x+1��+3a��x-2y��=16}\\{-b��x+1��+4��x-2y��=15}\end{array}\right.$�Ľ�Ϊ$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$��
��ѡ��B��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬��ʹ��������ÿ�����̵�����������ȵ�δ֪����ֵ���Ƿ�����Ľ⣮����Ĺؼ���Ҫ֪������������֮���Ĺ�ϵ��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
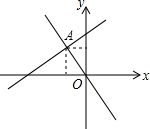 ��ͼ������y=-2x��y=kx+4��ͼ���ཻ�ڵ�A��m��3��������ڵ�x����ʽkx+4+2x��0�Ľ⼯Ϊx��-1.5��
��ͼ������y=-2x��y=kx+4��ͼ���ཻ�ڵ�A��m��3��������ڵ�x����ʽkx+4+2x��0�Ľ⼯Ϊx��-1.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2016x+m | B�� | y=$\frac{x}{2{x}^{2}+1}$+$\frac{m}{x}$ | C�� | y=x2-2016 | D�� | y=$\frac{{x}^{2}}{|x|}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 35��1-x��2=35-26 | B�� | 35��1-2x��=26 | C�� | 35��1-x��2=26 | D�� | 35��1-x2��=26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 A��B�������600ǧ�ף�һ���ͳ���A�ǿ���B�ǣ�����ΪÿСʱ80ǧ�ף�ͬʱһ�������B�ǿ���A�ǣ�����Ϊ��Сʱ100ǧ�ף���ͳ���ʱ��Ϊt��
A��B�������600ǧ�ף�һ���ͳ���A�ǿ���B�ǣ�����ΪÿСʱ80ǧ�ף�ͬʱһ�������B�ǿ���A�ǣ�����Ϊ��Сʱ100ǧ�ף���ͳ���ʱ��Ϊt���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com