
【题目】一手机经销商计划购进华为品牌![]() 型、
型、![]() 型、
型、![]() 型三款手机共
型三款手机共![]() 部,每款手机至少要购进
部,每款手机至少要购进![]() 部,且恰好用完购机款61000元.设购进
部,且恰好用完购机款61000元.设购进![]() 型手机
型手机![]() 部,
部,![]() 型手机
型手机![]() 部.三款手机的进价和预售价如下表:
部.三款手机的进价和预售价如下表:
手机型号 |
|
|
|
进价(单位:元/部) |
|
|
|
预售价(单位:元/部) |
|
|
|
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润W(元)与x(部)之间的关系式;
(注;预估利润W=预售总额![]() 购机款
购机款![]() 各种费用)
各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
【答案】(1)![]()
![]() ;(2)①
;(2)①![]() ②预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.
②预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.
【解析】
(1)关键描述语:A型、B型、C型三款手机共60部,由A、B型手机的部数可表示出C型的手机的部数.根据购机款列出等式可表示出x、y之间的关系.根据题干,求出x的取值范围.
(2)①由预估利润W=预售总额﹣购机款﹣各种费用,列出等式即可.
②利用一次函数的增减性,结合(1)中求得的x的取值范围,即可确定最大利润和各种手机的购买数量.
解:(1)C手机的部数为![]() ;因为购进手机总共用了61000原,所以
;因为购进手机总共用了61000原,所以
![]()
整理得,![]()
根据题意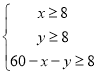 得:
得: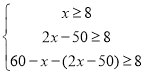
解得:![]()
故![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为:![]()
![]()
(2)①根据题意可知:
![]()
整理得,![]()
将(1)中![]() 代入以上关系式中,得
代入以上关系式中,得
![]()
整理得,
![]()
②根据![]() 可知:W是关于x的一次函数,且W随x的增大而增大
可知:W是关于x的一次函数,且W随x的增大而增大
∴当x=34时,W取最大值,![]()
将x=34分别代入![]() ,
,![]() 中,整理得:
中,整理得:
![]() ,
,![]()
即预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.


科目:初中数学 来源: 题型:
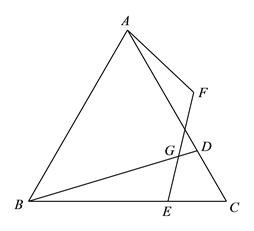
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
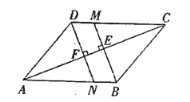
①求证:四边形![]() 是平行四边形;
是平行四边形;
②已知![]() ,求
,求![]() 的长.
的长.
(2)已知函数![]() .
.
①若函数图象经过原点,求![]() 的值
的值
②若这个函数是一次函数,且![]() 随着
随着![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
A、①②③B、①③⑤
C、②③④D、②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
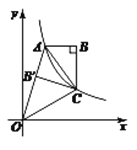
【题目】如图,双曲线![]() (
(![]() >0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与![]() 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥![]() 轴,将△ABC沿AC翻折后得△
轴,将△ABC沿AC翻折后得△![]() ,
,![]() 点落在OA上,则四边形OABC的面积是2,若BC=2,直线
点落在OA上,则四边形OABC的面积是2,若BC=2,直线![]() 与△ABC有交点,求
与△ABC有交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
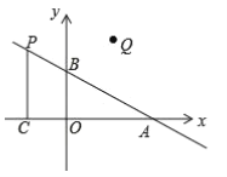
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:斜率表示一条直线y=kx+b(k≠0)关于橫坐标轴倾斜程度的量,即直线与x轴正方向夹角(倾斜角α)的正切值,表示成k=tanα。
(1)直线y=x-2b的倾斜角α=________。
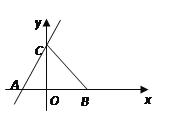
(2)如图,在△ABC中,tanA、tanB是方程x2-(![]() +1)x+
+1)x+![]() =0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
=0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com