
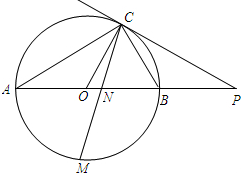
 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.分析 (1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;
(2)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MN•MC;代入数据可得MN•MC=BM2=8.
解答 (1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
(2)解:连接MA,MB,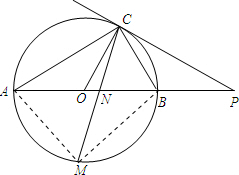
∵点M是$\widehat{AB}$的中点,
∴$\widehat{AM}=\widehat{BM}$.
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴$\frac{BM}{MC}$=$\frac{MN}{BM}$.
∴BM2=MN•MC.
又∵AB是⊙O的直径,$\widehat{AM}$=$\widehat{BM}$,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2$\sqrt{2}$.
∴MN•MC=BM2=8.
点评 此题主要考查圆的切线的判定及圆周角定理的运用和相似三角形的判定和性质的应用,证得BM2=MN•MC是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:单选题
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
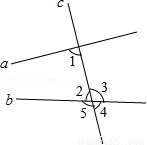
A. ∠2 B. ∠3 C. ∠4 D. ∠5
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
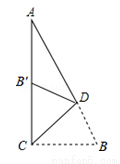
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD
折叠,使B点落在AC边上的B′处,则∠ADB′等于____°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
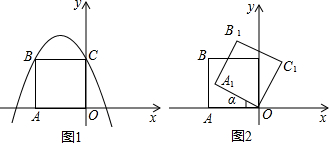
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com