
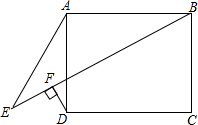
 如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF.
如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF. 分析 由矩形的性质得出AB=CD,∠BAD=90°,得出∠ABE+∠1=90°,再由已知条件得出AE=AB,由等腰三角形的性质得出∠E=∠ABE,证出∠ADF+∠2=90°,由对顶角相等得出∠ABE=∠ADF,即可得出结论.
解答 证明:如图所示: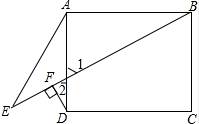
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=90°,
∴∠ABE+∠1=90°,
∵AE=CD,
∴AE=AB,
∴∠E=∠ABE,
∵DF⊥BE,
∴∠DFB=90°,
∴∠ADF+∠2=90°,
∵∠1=∠2,
∴∠ABE=∠ADF,
∴∠E=∠ADF.
点评 本题考查了矩形的性质、等腰三角形的判定与性质、角的互余关系;熟练掌握矩形的性质,证明三角形是等腰三角形是解决问题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:解答题
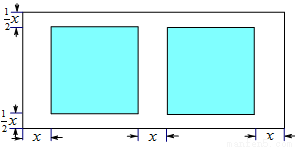
某小区有一块长18米,宽8米的长方形空地,计划在其中修建两块相同的长方形花圃.为方便游人观赏,准备在花圃周边修建如图所示的“两横三纵”人行通道,其中横向人行通道的宽度是纵向人行通道宽度的一半.设纵向人行通道的宽度为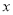 米,当
米,当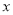 为何值时,花圃的面积之和为72米
为何值时,花圃的面积之和为72米 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
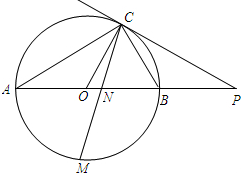 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com