
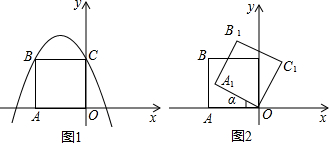
分析 (1)先求出点C的坐标,再根据正方形的边长相等,得出点B的坐标,代入y=ax2-2x+2,即可得出a的值.
(2)分两种情况求解:①当点E在抛物线顶点时;②当BC∥DE,且DE=BC=2时,即可求出答案;
(3)由点A1落在二次函数对称轴上,OA1=2,可得出∠A1OA=60°,进而得出∠BOB1=60°,求出∠B1OC=15°,利用三角函数表示点B1的坐标即可.
解答 解:(1)二次函数y=ax2-2x+2的图象与y轴交于点C,
∴C(0,2),
∵以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
∴B(-2,2),把B(-2,2)代入y=ax2-2x+2,得2=4a+4+2,解得a=-1.
(2)①当点E在抛物线顶点时,
∵二次函数的解析式为y=-x2-2x+2.
∴E(-1,3)
∵点D在二次函数的对称轴上,
∴当E(-1,3)以B,C,D,E四点为顶点的四边形为平行四边形
②当BC∥DE,且DE=BC=2时,
∵点D在二次函数的对称轴上,
∴D的横坐标为-1,
∴设点E的横坐标为t,则有-1-t=2,或t-(-1)=2,解得t=-3或1.
∴E(-3,-1)或(1,-1)
综上所述:当点E的坐标为(-1,3)或(-3,-1)或(1,-1),以B,C,D,E四点为顶点的四边形为平行四边形.
(3)如图1,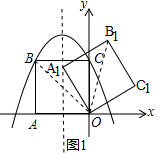
∵点A1落在二次函数对称轴上,OA1=2
∴∠A1OA=60°,
∴∠BOB1=60°,
∴∠B1OC=60°-45°=15°,
∵OB1=OB=2$\sqrt{2}$,
∴B1(2$\sqrt{2}$sin15°,2$\sqrt{2}$cos15°).
点评 本题主要考查了二次函数综合题,求二次函数图象与坐标轴的交点,正方形的性质,配方法,相似三角形的判定与性质,锐角三角函数,等腰直角三角形的性质,难点在于第(2)小题的两个小题都要分情况讨论,并且运算量较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:判断题
(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
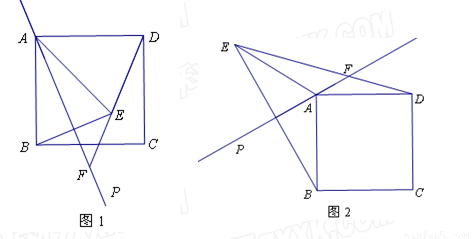
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且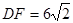 ,
,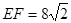 ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
下列式子不能因式分解的是( )
A. x2-4 B. 3x2+2x C. x2+25 D. x2-4x+4
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
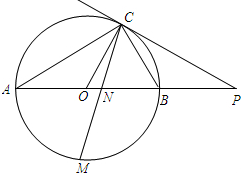 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com