Question

13．一个矩形ABCD的较短边长为2．
（1）如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长2$\sqrt{2}$；
（2）如图②，已知矩形ABCD的另一边长为4，剪去一个矩形ABEF后，余下的矩形EFDC与原矩形相似，求余下矩形EFDC的面积2．

Answer 1

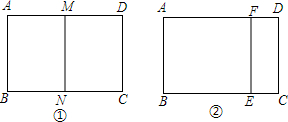
分析 （1）设它的另一边长为2x，则AM=DM=x，根据相似多边形的性质得$\frac{AM}{AB}$=$\frac{AB}{AD}$，即$\frac{x}{2}$=$\frac{2}{2x}$，然后解方程求出x则可得到矩形ABCD的另一边长；
（2）设DF=a，根据相似多边形的性质得$\frac{CD}{AD}$=$\frac{DF}{AB}$，即$\frac{2}{4}$=$\frac{DF}{2}$，然后利用比例性质求出DF，再利用矩形面积公式计算矩形EFDC的面积．

解答 解：（1）设它的另一边长为2x，则AM=DM=x，
∵矩形ABNM与矩形ADCB相似，
∴$\frac{AM}{AB}$=$\frac{AB}{AD}$，即$\frac{x}{2}$=$\frac{2}{2x}$，解得x=$\sqrt{2}$，
∴矩形ABCD的另一边长为2$\sqrt{2}$；
（2）设DF=a，
∵余下的矩形EFDC与矩形ADCB相似，
∴$\frac{CD}{AD}$=$\frac{DF}{AB}$，即$\frac{2}{4}$=$\frac{DF}{2}$，解得DF=1，
∴矩形EFDC的面积=2×1=2．
故答案为2$\sqrt{2}$，2．

点评 本题考查了相似多边形的性质：如果两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形；相似多边形对应边的比叫做相似比．