
| ���� | �� | �¿��� | ŦԼ | Ϥ�� |
| ʱ�� | -7 | +4 | -12 | +2 |
���� ��1�����������г���ʽ7��30+��-7����7��30+4��7��30+2��������ɣ�
��2�����9+13�����ɵõ�����ʱ����7��16��22ʱ���ٸ���22+��-12���������ŦԼ��ʱ�䣻
��3���������ʱ��7��19������2��ŦԼ��ʱ��[2+12+��-12��]���ٿ�������Ƿ���ʼ��ɣ�
��� �⣺��1��7��30+��-7��=0��30��7��30+4=11��30��7��30+2=9��30��
�𣺴�ʱ��ʱ��Ϊ6��20���賿0��30���¿���ʱ��Ϊ6��20������11��30��Ϥ���ʱ��Ϊ6��20������9��30��
��2��9+13=22��
22+��-12��=10��
��ŦԼ��ʱ����7��16������10ʱ��
��3��2+12+��-12��=2��ŦԼʱ��Ϊ7��19���賿2ʱ��
�ʲ����ʣ�
���� ���⿼�����������ļӼ��������������������ȵ�Ӧ�ã��ؼ����������⣬���������г���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�ζ��о��꼶��ѧ�ڵ�һ��ѧ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
����ʽ�Ӳ�����ʽ�ֽ����( )
A. x2��4 B. 3x2��2x C. x2��25 D. x2��4x��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
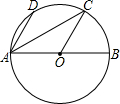 ��ͼ��AB�ǡ�O��ֱ������D��C�ڡ�O�ϣ�AD��OC����DAB=60�㣬����AC�����DAC���ڣ�������
��ͼ��AB�ǡ�O��ֱ������D��C�ڡ�O�ϣ�AD��OC����DAB=60�㣬����AC�����DAC���ڣ�������| A�� | 20�� | B�� | 30�� | C�� | 25�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com