【题目】如图，矩形ABCD中，AB=8，点E是AD上的一点，有AE=4，BE的垂直平分线交BC的延长线于点F，连结EF交CD于点G．若G是CD的中点，则BC的长是 ．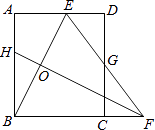 
【答案】7
【解析】解：∵矩形ABCD中，G是CD的中点，AB=8， ∴CG=DG= 
×8=4，
在△DEG和△CFG中，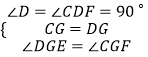
，
∴△DEG≌△CFG（ASA），
∴DE=CF，EG=FG，
设DE=x，
则BF=BC+CF=AD+CF=4+x+x=4+2x，
在Rt△DEG中，EG= 
= 
，
∴EF=2 ，
∵FH垂直平分BE，
∴BF=EF，
∴4+2x=2 ，
解得x=3，
∴AD=AE+DE=4+3=7，
∴BC=AD=7．
故答案为：7．
根据线段中点的定义可得CG=DG，然后利用“角边角”证明△DEG和△CFG全等，根据全等三角形对应边相等可得DE=CF，EG=FG，设DE=x，表示出BF，再利用勾股定理列式求EG，然后表示出EF，再根据线段垂直平分线上的点到两端点的距离相等可得BF=EF，然后列出方程求出x的值，从而求出AD，再根据矩形的对边相等可得BC=AD．
名校课堂系列答案科目：初中数学 来源： 题型：
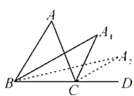
【题目】如图，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线交于点A1，得∠A1，∠A1BC和∠A1CD的平分线交于点A2，得∠A2…∠A2 017BC和∠A2 017CD的平分线交于点A2 018，则∠A2 018＝_____度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，梯形OABC中，BC∥AO，O（0，0），A（10，0），B（10，4），BC=2，G（t，0）是底边OA上的动点． 
（1）tan∠OAC= ．
（2）边AB关于直线CG的对称线段为MN，若MN与△OAC的其中一边平行时，则t=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（提出问题）
如图①，点
、
、
在同一条直线上，
，
，且
，
，易证
≌
．
（类比探究）
（
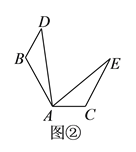
）如图②，在和中，，若
，
，
．求证：≌．
（知识应用）
（
）如图②，在和中，，若，，，若
的度数是
的
倍，则
__________
．
（数学思考）
（
）如图②，在和中，，若
，
，当≌时，
__________．（结果用含有
的代数式表示）
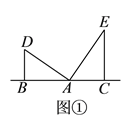
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BE=BF．
（1）求证：四边形BDEF为平行四边形；
（2）当∠C=45°，BD=2时，求D，F两点间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
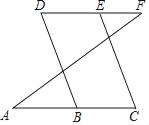
【题目】填写理由：如图所示
∵DF∥AC（已知），
∴∠D+∠DBC=180°．（ ）
∵∠C=∠D（已知），
∴∠C+ =180°．（ ）
∴DB∥EC（ ）
∴∠D=∠CEF．（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
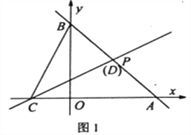
【题目】如图，直线l1经过过点P（2，2），分别交x轴、y轴于点A（4，0），B。
（1）求直线l1的解析式；
（2）点C为x轴负半轴上一点，过点C的直线l2：
交线段AB于点D。
如图1，当点D恰与点P重合时，点Q（t，0）为x轴上一动点，过点Q作QM⊥x轴，分别交直线l1、l2于点M、N。若
，MN=2MQ，求t的值；
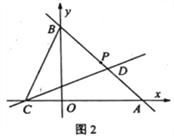
如图2，若BC=CD，试判断m，n之间的数量关系并说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，PA、PB分别与⊙O相切于点A、B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N． 
（1）求证：OM=AN；
（2）若⊙O的半径R=3，PA=9，求OM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，∠BAC=30°，AB=8，AD平分∠BAC，点PQ分别是AB、AD边上的动点，则PQ+BQ的最小值是
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com