
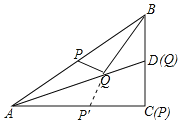
【题目】如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是

A. 4 B. 5 C. 6 D. 7
【答案】A
【解析】
如图,作点P关于直线AD的对称点P′,连接QP′,由△AQP≌△AQP′,得PQ=QP′,欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,即当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.
如图,作点P关于直线AD的对称点P′,连接QP′,
在△AQP和△AQP′中,
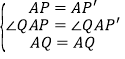 ,
,
∴△AQP≌△AQP′,
∴PQ=QP′
∴欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,
∴当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长。
在Rt△ABC中,∵∠C=90°,AB=8,∠BAC=30°,
∴BC=![]() AB=4,
AB=4,
∴PQ+BQ的最小值是4,
故选A.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 . 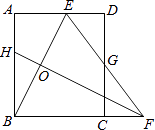
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学每天中午总是在规定时间打开学校大门,七年级同学小明每天中午同一时间从家骑自行车到学校,星期一中午他以每小时15千米的速度到校,结果在校门口等了6分钟才开门,星期二中午他以每小时9千米的速度到校,结果校门已开了6分钟,星期三中午小明想准时到达学校门口,那么小明骑自行车的速度应该为每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AB=10,BC=6,
(1)计算AC的长度;
(2)计算AB边上的中线CD的长度.
(3)计算AB边上的高CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE= . 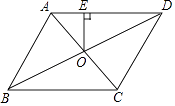
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是 . 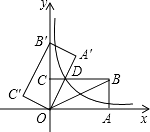
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com